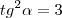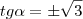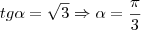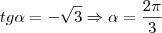por rodsales » Dom Jun 28, 2009 20:25
por rodsales » Dom Jun 28, 2009 20:25
Os valores de

, com

e

, dada por

, assume valor mínimo igual a -4 são:
Eu cheguei ao resultado de

mas não entendi por que o livro deu a resposta também de

.
Grato,
Aguardo respostas.
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por DanielFerreira » Qui Jul 30, 2009 18:45
por DanielFerreira » Qui Jul 30, 2009 18:45
- ? = - 4 * 4a
? = 16a
16 + 16 * tg² a = 16*4
1 + tg² a = 4
tg² a = 3
tg a = ?3
a = 60°
180° ---- ?
60° ----- k
180k = 60?
18k = 6?
k = ?/3
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Molina » Qui Jul 30, 2009 20:07
por Molina » Qui Jul 30, 2009 20:07
Boa noite.
Realmente são as duas soluções.
A Báskhara feita pelo nosso amigo a cima está correta até o seguinte ponto:
danjr5 escreveu:- ? = - 4 * 4a
? = 16a
16 + 16 * tg² a = 16*4
1 + tg² a = 4
tg² a = 3
A partir daqui faltou ele considerar que:
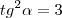
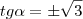
Ou seja,
mais ou menor raiz de três.
Considerando o intervalo dado temos que
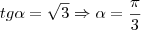
e
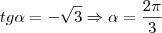
Na dúvida faça o ciclo trigonométrico que você vai visualizar com facilidade.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por DanielFerreira » Sex Jul 31, 2009 13:09
por DanielFerreira » Sex Jul 31, 2009 13:09
ok.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determine os valores de m
por manuoliveira » Qui Mai 06, 2010 17:48
- 3 Respostas
- 2313 Exibições
- Última mensagem por MarceloFantini

Sáb Mai 08, 2010 00:40
Trigonometria
-
- Dúvida em valores de seno, cosseno e tangente.
 por Sobreira » Ter Abr 30, 2013 00:40
por Sobreira » Ter Abr 30, 2013 00:40
- 1 Respostas
- 1390 Exibições
- Última mensagem por young_jedi

Ter Abr 30, 2013 12:52
Trigonometria
-
- Quais os possíveis valores que satisfazem os valores reais
por andersontricordiano » Seg Fev 24, 2014 22:53
- 1 Respostas
- 5159 Exibições
- Última mensagem por Russman

Ter Fev 25, 2014 02:17
Números Complexos
-
- Os valores de x são?
por Killder » Ter Nov 27, 2012 08:11
- 1 Respostas
- 2811 Exibições
- Última mensagem por Neperiano

Ter Nov 27, 2012 15:09
Álgebra Elementar
-
- valores: x e de y
por Victor Gabriel » Dom Abr 21, 2013 16:02
- 1 Respostas
- 2567 Exibições
- Última mensagem por Luis Gustavo

Seg Mai 06, 2013 16:48
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , com
, com  e
e  , dada por
, dada por  , assume valor mínimo igual a -4 são:
, assume valor mínimo igual a -4 são: mas não entendi por que o livro deu a resposta também de
mas não entendi por que o livro deu a resposta também de  .
.
 , com
, com  e
e  , dada por
, dada por  , assume valor mínimo igual a -4 são:
, assume valor mínimo igual a -4 são: mas não entendi por que o livro deu a resposta também de
mas não entendi por que o livro deu a resposta também de  .
.