smlspirit escreveu:Não consigo desenvolver o seguinte problema:
Dividindo um número de dois algarismo, cuja soma é 9, pelo quociente da divisão do algarismo das unidades pelo algarismo das dezenas, obtém-se o quociente 18. Qual é esse número?
Gostaria de uma ajuda para compreender o problema e montar a equação.
Obrigado
Seja esse número

. Como ele tem apenas dois algarismos, sejam eles

e

, podemos escrever que
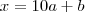
. Concorda?
Assim, vamos ao enunciado! Ele nos dá duas informações:
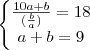
Eu acho interessante fato de que se a soma dos algarismos de um número é 9 então este é múltiplo de 9. Veja que isto nos dá apenas algumas combinações específicas para (a,b). Assim, podíamos fazer tentativas e verificar qual par satisfaz a equação 1. Maaaaaas, vamos recorrer a boa e confiável álgebra.
Da equação 1, podemos desenvolver que
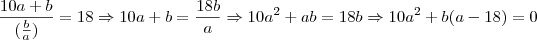
.
Pela equação 2 sabemos que a e b se relacionam seguindo
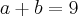
. Portanto, se tomarmos
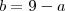
e substituirmos na equação acima teremos uma equação de 2° grau na incógnita a!
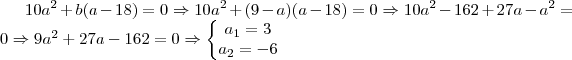
Como

deve ser um algarismo, a única solução válida é

. Agora, como eu sei que
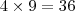
é fácil imaginar que

, pelo argumento que eu dei acima. Claro,

.
Portanto, o seu número é 36!


 . Como ele tem apenas dois algarismos, sejam eles
. Como ele tem apenas dois algarismos, sejam eles  e
e  , podemos escrever que
, podemos escrever que 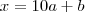 . Concorda?
. Concorda?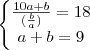
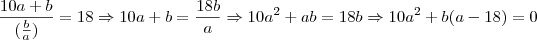 .
.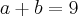 . Portanto, se tomarmos
. Portanto, se tomarmos 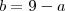 e substituirmos na equação acima teremos uma equação de 2° grau na incógnita a!
e substituirmos na equação acima teremos uma equação de 2° grau na incógnita a! 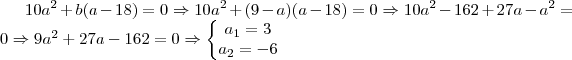
 . Agora, como eu sei que
. Agora, como eu sei que 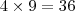 é fácil imaginar que
é fácil imaginar que  , pelo argumento que eu dei acima. Claro,
, pelo argumento que eu dei acima. Claro,  .
.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.