 por bmachado » Seg Jun 11, 2012 16:29
por bmachado » Seg Jun 11, 2012 16:29
O cerimonial de um evento deve acomodar 4 delegações.
Sabe-se que o evento contará com a participação de 5 representantes de MG, 4 de SP, 7 do RJ e 6 do CE.
Para acomodar os participantes, foram separadas 22 poltronas, cada uma com o nome do respectivo participante.
Porém, os representante do CE e SP desejam sentar-se juntos, enquanto as demais delegações não fizeram tal exigência.
O total de maneiras do cerimonial posicionar os participantes na fileira, atendendo às condições apresentadas, é dado por:
a) 14! 6! 4!
b) 22! 6! 4!
c) 5! 7! 6! 4!
d) 10! 6! 4!
Gabarito(correto) "(a)", tentei e achei "(c)" !?
Obrigado.
-
bmachado
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Fev 29, 2012 00:28
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: EF
- Andamento: formado
 por fraol » Qua Jun 13, 2012 20:57
por fraol » Qua Jun 13, 2012 20:57
Boa noite,
Como os representantes de CE vão sentar-se juntos, imaginemos que temos uma grande poltrona para as 6 pessoas.
Como os representantes de SP vão sentar-se juntos, imaginemos que temos uma grande poltrona para as 4 pessoas.
Para os demais teremos 12 poltronas, uma para cada pessoa.
Então no total seriam permutados 14 lugares, isto é
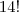
.
Mas os representantes de CE e SP devem ser permutados também =>
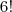
e
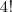
.
Juntando tudo dá
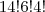
.
Na sua solução você mantém os representantes de MG e RJ juntos. Mas essa não é uma condição do problema, certo?
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por bmachado » Qua Jun 13, 2012 22:03
por bmachado » Qua Jun 13, 2012 22:03
Obrigado pelo contribuição, resolução sucinta e de fácil compreensão, abs.
fraol escreveu:Boa noite,
Como os representantes de CE vão sentar-se juntos, imaginemos que temos uma grande poltrona para as 6 pessoas.
Como os representantes de SP vão sentar-se juntos, imaginemos que temos uma grande poltrona para as 4 pessoas.
Para os demais teremos 12 poltronas, uma para cada pessoa.
Então no total seriam permutados 14 lugares, isto é
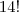
.
Mas os representantes de CE e SP devem ser permutados também =>
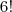
e
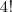
.
Juntando tudo dá
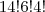
.
Na sua solução você mantém os representantes de MG e RJ juntos. Mas essa não é uma condição do problema, certo?
.
-
bmachado
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Fev 29, 2012 00:28
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: EF
- Andamento: formado
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Probabilidade difícil
por joaofonseca » Qua Mar 21, 2012 13:28
- 1 Respostas
- 1565 Exibições
- Última mensagem por joaofonseca

Sex Mar 23, 2012 18:19
Probabilidade
-
- questão dificil.
por natanskt » Seg Dez 13, 2010 18:20
- 1 Respostas
- 2455 Exibições
- Última mensagem por Molina

Sáb Dez 25, 2010 20:28
Binômio de Newton
-
- Questão dificil
por cortelettirlz » Qua Set 07, 2011 15:32
- 1 Respostas
- 1611 Exibições
- Última mensagem por MarceloFantini

Dom Set 11, 2011 19:43
Sistemas de Equações
-
- Questão Difícil
por Bira » Dom Ago 12, 2012 17:55
- 0 Respostas
- 1330 Exibições
- Última mensagem por Bira

Dom Ago 12, 2012 17:55
Probabilidade
-
- Retas questão dificil
por o_andrade » Qui Jul 28, 2011 22:06
- 1 Respostas
- 1491 Exibições
- Última mensagem por o_andrade

Qui Jul 28, 2011 23:04
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


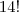 .
.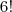 e
e 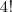 .
.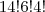 .
.

 .
.



