 por PeterHiggs » Qui Jun 07, 2012 13:36
por PeterHiggs » Qui Jun 07, 2012 13:36
ABCD é um quadrado, DM = MC e AE = CE + CB. Calcule

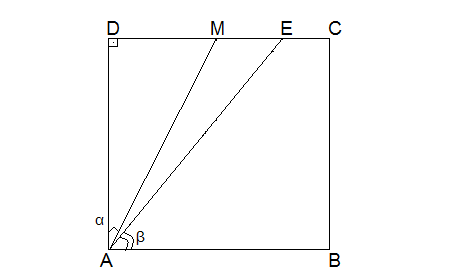
- 1) ABCD é um quadrado ....png (6.3 KiB) Exibido 10789 vezes
Resposta: 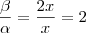
Bom, tentei resolver de todas as formas possíveis, mas não consegui.
Ali abaixo está o quadrado, e a minha tentativa de resolução. Tentei chegar a um ponto em que isolasse alfa e beta na mesma variável, como está na resposta, mas não obtive resultado!
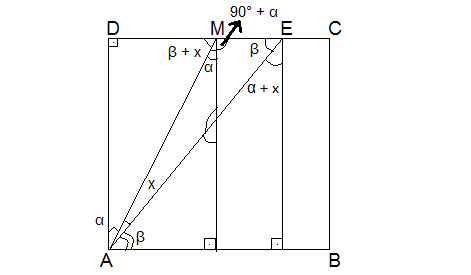
- ABCD é um quadrado ....png (8.59 KiB) Exibido 10789 vezes
Alguém pode me ajudar? Obrigado
-
PeterHiggs
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Mai 25, 2012 18:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Dom Jun 10, 2012 18:07
por DanielFerreira » Dom Jun 10, 2012 18:07
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por PeterHiggs » Dom Jun 10, 2012 19:39
por PeterHiggs » Dom Jun 10, 2012 19:39
Olá, muito obrigado pela ajuda e pelos cálculos na folha scanneada.
Eu ia te perguntar uma coisa, danjr5: aquela relação que você colocou:
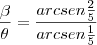
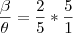
= 2
Ela é válida matematicamente?
-
PeterHiggs
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Mai 25, 2012 18:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Dom Jun 10, 2012 20:39
por DanielFerreira » Dom Jun 10, 2012 20:39
PeterHiggs,
já que perguntou; acho que não. Fui tentado a fazer isso - coincidia com o gabarito.
Dedicarei uma parte do meu tempo amanhã afim de apresentar-lhe uma solução mais satisfatória. A propósito, desconsidere meu primeiro post .
Até breve!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Seg Jun 11, 2012 23:57
por DanielFerreira » Seg Jun 11, 2012 23:57
E aí Peter, blz?!
Acho que agora foi! Rsrsrs
Considere:
ME = x
EC = y
CB = z
Do enunciado temos:
DM = x + y
AE = y + z
Considerando a figura digitalizada, do triângulo
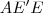
concluímos que:
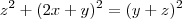
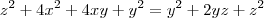
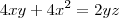
Substituindo
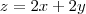
(quadrado)
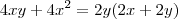



=> A abertura do ângulo

indica

, ou seja,
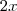
=> A abertura do ângulo

indica

, ou seja,

Daí,
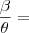
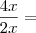

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por PeterHiggs » Ter Jun 12, 2012 13:11
por PeterHiggs » Ter Jun 12, 2012 13:11
Muito obrigado pela resposta, danjr5 .
-
PeterHiggs
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Mai 25, 2012 18:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Pentágono determinar o valor de beta
 por felipegserrano » Sáb Fev 15, 2014 13:29
por felipegserrano » Sáb Fev 15, 2014 13:29
- 1 Respostas
- 1442 Exibições
- Última mensagem por felipegserrano

Dom Fev 16, 2014 04:46
Geometria Plana
-
- Alfa de Cronbach
por sil_nana » Sex Jun 11, 2010 16:06
- 0 Respostas
- 3221 Exibições
- Última mensagem por sil_nana

Sex Jun 11, 2010 16:06
Estatística
-
- Determine alfa - Vetores
 por PeterHiggs » Qui Jan 03, 2013 22:14
por PeterHiggs » Qui Jan 03, 2013 22:14
- 1 Respostas
- 1564 Exibições
- Última mensagem por young_jedi

Sáb Jan 05, 2013 16:16
Álgebra Linear
-
- Calcular o Cos (alfa-5Beta)
por darkthorn » Ter Nov 19, 2013 12:55
- 0 Respostas
- 1136 Exibições
- Última mensagem por darkthorn

Ter Nov 19, 2013 12:55
Trigonometria
-
- calcular K sabendo a tangente de (alfa/2)
por darkthorn » Seg Out 28, 2013 09:37
- 1 Respostas
- 2042 Exibições
- Última mensagem por darkthorn

Ter Out 29, 2013 23:44
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

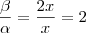


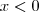 , mas...
, mas...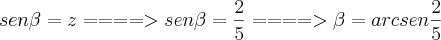

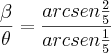
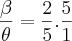
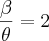

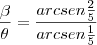
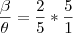 = 2
= 2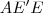 concluímos que:
concluímos que: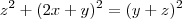
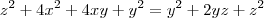
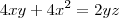
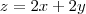 (quadrado)
(quadrado)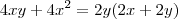



 indica
indica  , ou seja,
, ou seja, 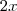
 indica
indica  , ou seja,
, ou seja, 
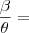
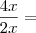

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.