 por Luiz Felipe » Ter Jun 05, 2012 22:48
por Luiz Felipe » Ter Jun 05, 2012 22:48
Uma folha de papel ABCD de formato retangular é dobrada em torno do segmento EF, de maneira que o ponto A ocupe a posição G, como mostra a figura. Se AE = 3 e BG = 1, então a medida do segmento AF é igual a :
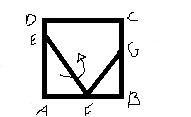
- FIGURA
- Figura.JPG (4.12 KiB) Exibido 7834 vezes
RESP.:
![\frac{(3\sqrt[2]{5})}{5} \frac{(3\sqrt[2]{5})}{5}](/latexrender/pictures/9d5efe0f4f83b392ec934d88826d560c.png)
Esta questão eu não consegui começar tambem.
Eu começei a estudar Geometria Plana hoje, nunca tinha estudado antes, conto com a ajuda de vocês para sanar minhas duvidas.

-
Luiz Felipe
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Fev 13, 2012 15:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Ciências Biologicas
- Andamento: cursando
 por MarceloFantini » Qua Jun 06, 2012 02:45
por MarceloFantini » Qua Jun 06, 2012 02:45
É muito importante lembrar que ele dobrou a página, pois isto significa que

e

. Trace uma reta paralela a
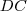
começando no ponto
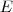
e chame este novo ponto de
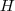
. Temos que
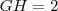
pois

. O triângulo retângulo
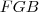
tem hipotenusa

e um cateto

. Usando o teorema de pitágoras, chegamos que o outro cateto é
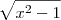
.
Assim, o segmento
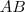
tem comprimento
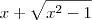
, mesmo comprimento de
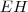
. Preste atenção ao triângulo
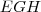
que criamos. Ele é retângulo, tem hipotenusa 3, catetos 2 e
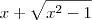
. Aplicando o teorema de pitágoras, vem
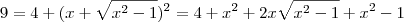
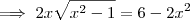
.
Elevando os dois lados ao quadrado, segue
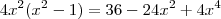
;
dividindo por 4,
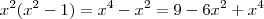
que nos leva a
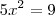
e finalmente
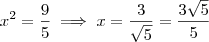
, pois

é um comprimento e portanto positivo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em geometria plana
 por tadeutato » Seg Abr 25, 2011 11:26
por tadeutato » Seg Abr 25, 2011 11:26
- 2 Respostas
- 1669 Exibições
- Última mensagem por SidneySantos

Seg Abr 25, 2011 22:33
Geometria Plana
-
- Duvida - Geometria Plana
 por Luiz Felipe » Ter Jun 05, 2012 21:32
por Luiz Felipe » Ter Jun 05, 2012 21:32
- 2 Respostas
- 2830 Exibições
- Última mensagem por Pandaludo

Ter Ago 06, 2013 17:31
Geometria Plana
-
- Duvida - Geometria Plana 2
 por Luiz Felipe » Ter Jun 05, 2012 22:27
por Luiz Felipe » Ter Jun 05, 2012 22:27
- 1 Respostas
- 1135 Exibições
- Última mensagem por MarceloFantini

Qua Jun 06, 2012 02:38
Geometria Plana
-
- [Geometria Plana] Duvida
 por Micael » Qui Mar 14, 2013 17:57
por Micael » Qui Mar 14, 2013 17:57
- 1 Respostas
- 1095 Exibições
- Última mensagem por timoteo

Qui Mar 14, 2013 18:34
Geometria Plana
-
- [Geometria Plana] DÚVIDA
 por Micael » Seg Mai 13, 2013 19:38
por Micael » Seg Mai 13, 2013 19:38
- 1 Respostas
- 2734 Exibições
- Última mensagem por Molina

Seg Mai 13, 2013 23:35
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{(3\sqrt[2]{5})}{5} \frac{(3\sqrt[2]{5})}{5}](/latexrender/pictures/9d5efe0f4f83b392ec934d88826d560c.png)


![\frac{(3\sqrt[2]{5})}{5} \frac{(3\sqrt[2]{5})}{5}](/latexrender/pictures/9d5efe0f4f83b392ec934d88826d560c.png)


 e
e  . Trace uma reta paralela a
. Trace uma reta paralela a 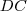 começando no ponto
começando no ponto 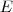 e chame este novo ponto de
e chame este novo ponto de 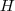 . Temos que
. Temos que 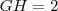 pois
pois  . O triângulo retângulo
. O triângulo retângulo 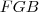 tem hipotenusa
tem hipotenusa  e um cateto
e um cateto  . Usando o teorema de pitágoras, chegamos que o outro cateto é
. Usando o teorema de pitágoras, chegamos que o outro cateto é 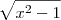 .
.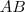 tem comprimento
tem comprimento 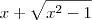 , mesmo comprimento de
, mesmo comprimento de 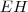 . Preste atenção ao triângulo
. Preste atenção ao triângulo 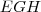 que criamos. Ele é retângulo, tem hipotenusa 3, catetos 2 e
que criamos. Ele é retângulo, tem hipotenusa 3, catetos 2 e 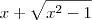 . Aplicando o teorema de pitágoras, vem
. Aplicando o teorema de pitágoras, vem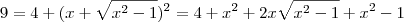
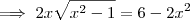 .
.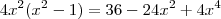 ;
;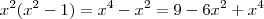
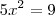 e finalmente
e finalmente 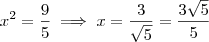 , pois
, pois  é um comprimento e portanto positivo.
é um comprimento e portanto positivo.






