 por Priscilamoraes307 » Sex Jun 01, 2012 20:35
por Priscilamoraes307 » Sex Jun 01, 2012 20:35
Determine

para que o SISTEMA tenha solução única:

= 4
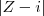
=

Só consegui fazer que

= x² + y² = 16 raio = 4
é uma equação da circunferência com raio = 4 ? Tenho que achar o afixo? como faço para achar o angulo?
Obrigada!!!!!!!
-
Priscilamoraes307
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jun 01, 2012 20:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Sáb Jun 02, 2012 03:15
por Russman » Sáb Jun 02, 2012 03:15
Sim, o módulo de z ser 4 implica que você está considerando o conjunto de números complexos que distam 4 unidades da origem. Ou seja, uma circunferência de raio 4.
Agora, a segunda informação diz que se você sutrái i de z ele deve calcular um módulo beta. Vamos ver oq isso significa:
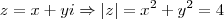
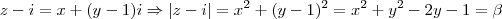
Da 1° equação, sabemos que x² + y² = 4. Apliquemos então na segunda equação esse resultado.
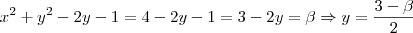
O que me vem a mente é que para z ser complexo então y dever ser não nulo. Assim temos
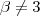
.
"Solução única" seria selecionar somente 1 complezo de módulo 4. Não sei...
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por MarceloFantini » Sáb Jun 02, 2012 12:45
por MarceloFantini » Sáb Jun 02, 2012 12:45
Você quer duas circunferências tangentes. Uma tem centro na origem e raio 4 enquanto que a outra tem centro em

e raio a determinar. Pela configuração do problema, vemos que a solução é
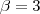
. Mas a circunferência pode tangenciar inferiormente apenas, logo
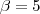
também.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Russman » Sáb Jun 02, 2012 19:54
por Russman » Sáb Jun 02, 2012 19:54
Áh, sim! Eu escrevi errado a segunda equação. O correto seria
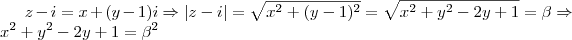
Fazendo o mesmo processo que anteriormente, obtemos
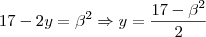
.
Agora aplicando este resultado na 1° equação, faz-se uma euqção em x
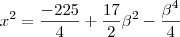
que tem duas soluções:
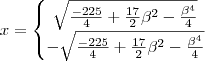
de onde existira resposta única para o problema quando forem iguais. Logo,
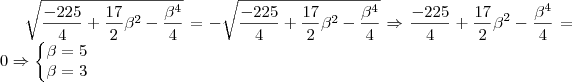
.
Portanto, a solução pra o seu problema é
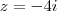
, se
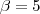
e
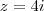
se
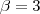
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17117 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- Numeros complexos!
por Estela » Seg Mar 17, 2008 00:57
- 7 Respostas
- 13356 Exibições
- Última mensagem por andegledson

Seg Nov 02, 2009 21:41
Números Complexos
-
- Números Complexos
por michelle » Dom Ago 31, 2008 15:35
- 3 Respostas
- 10333 Exibições
- Última mensagem por admin

Dom Ago 31, 2008 21:00
Números Complexos
-
- Números Complexos
por Cleyson007 » Qui Mai 14, 2009 13:57
- 7 Respostas
- 13957 Exibições
- Última mensagem por Cleyson007

Sáb Mai 16, 2009 11:04
Números Complexos
-
- NUMEROS COMPLEXOS
por lieberth » Sáb Jun 13, 2009 13:48
- 1 Respostas
- 4111 Exibições
- Última mensagem por Marcampucio

Sáb Jun 13, 2009 14:35
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 para que o SISTEMA tenha solução única:
para que o SISTEMA tenha solução única: = 4
= 4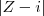 =
= 
 = x² + y² = 16 raio = 4
= x² + y² = 16 raio = 4 
 para que o SISTEMA tenha solução única:
para que o SISTEMA tenha solução única: = 4
= 4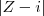 =
= 
 = x² + y² = 16 raio = 4
= x² + y² = 16 raio = 4 
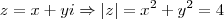
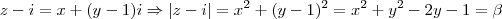
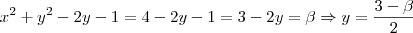
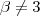 .
.
 e raio a determinar. Pela configuração do problema, vemos que a solução é
e raio a determinar. Pela configuração do problema, vemos que a solução é 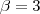 . Mas a circunferência pode tangenciar inferiormente apenas, logo
. Mas a circunferência pode tangenciar inferiormente apenas, logo 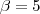 também.
também.

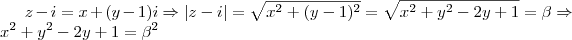
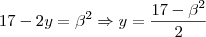 .
.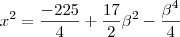
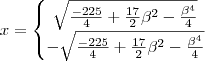
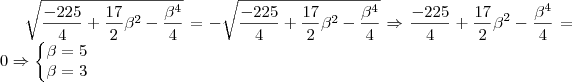 .
.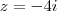 , se
, se 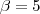 e
e 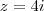 se
se 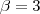 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
