Bom dia, Estou aprendendo derivada e gostaria de ajuda com essas questões.. agluém pode me explicar por favor?
Ache a primeira derivada em relação a para cada uma das seguintes funções .
a) y= -2^5 + 3x^3 - raiz quadrada 2x
Desculpem, mas não sei colocar o simbolo de raiz quadrada, nem elevar os numeros, então o numero elevado está com o simbolo antes de ^.
Grata


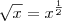
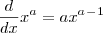 , mas também podemos utilizar a regra da cadeia para essa forma, no entanto, nesse caso, é mais conveniente transformar a raíz em potência.
, mas também podemos utilizar a regra da cadeia para essa forma, no entanto, nesse caso, é mais conveniente transformar a raíz em potência.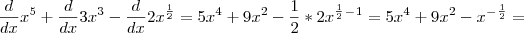
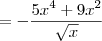


 .
.



