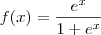
Calculando o limite quando
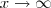 , eu encontro facilmente 1.
, eu encontro facilmente 1.No entanto, eu estou tentando calcular o limite quando
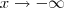 encontrando 1 também, mas de acordo com o gabarito e o "wolfram", dá 0.
encontrando 1 também, mas de acordo com o gabarito e o "wolfram", dá 0.Eu não entendi exatamente o por quê de dar 0. Já analisei o comportamento da função de diversas maneiras, se alguém puder me explicar o que acontece e também puder dar algum outro exemplo(se puder, caso não souber, não tem problema) em que esse mesmo comportamento ocorre, por favor... :/


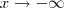 , temos que
, temos que  e
e 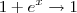 , logo
, logo 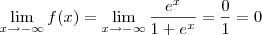 .
.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)