Probabilidade ( prova de Vestibular Fatec)

[PAULOMMS]

Por Favor me ajudem nesta Questão ...


Admita que, na FATEC-SP, há uma turma de
40 alunos de Logística, sendo 18 rapazes; e uma
turma de 36 alunos de Análise de Sistemas, sendo
24 moças. Para participar de um debate serão
escolhidos aleatoriamente dois alunos, um de cada
turma. Nessas condições, a probabilidade de que
sejam escolhidos uma moça e um rapaz é?

[joaofonseca]

Como eu gostaria que todas as questões do exame nacional de Matemática fossem como esta!!

1)De cada turma será escolhido um aluno. Logo os casos possiveis são

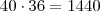
2)Em relação ao casos favoráveis temos de considerar de onde será escolhido o rapaz e a rapariga.

3)Se a rapariga for escolhida da 1ª turma, temos .

4)Se a rapariga for escolhida da 2ª turma, temos .

5)Somando 3) e 4) ficamos com 696 casos favoráveis

Agora é aplicar a definição de probabilidade segundo Laplace!