Propriedade de reflexão das conicas

[CarolMarques]

A planta baixa de um muro tem a forma de um ramo de hipérbole.Bernardes , encostado ao muro , foi atingido por um tiro disparado por Arthur , que ocupava o foco.Durante o inquérito policial, Arthur alegou que fora um acidente:a bala ricocheteara após atingir o muro , ferindo Bernardes.Admitindo que a propriedade de reflexão é válida para a bala , prove que Arthur mentiu.

A questão não vem com figura só com enunciado.Eu sei que deve ser aplicado os conceitos da propriedades de reflexão das cônicas mas não sei como começar a questão.Por favor me ajudem.

[LuizAquino]

A planta baixa de um muro tem a forma de um ramo de hipérbole.Bernardes , encostado ao muro , foi atingido por um tiro disparado por Arthur , que ocupava o foco.Durante o inquérito policial, Arthur alegou que fora um acidente:a bala ricocheteara após atingir o muro , ferindo Bernardes.Admitindo que a propriedade de reflexão é válida para a bala , prove que Arthur mentiu.

A questão não vem com figura só com enunciado. Eu sei que deve ser aplicado os conceitos da propriedades de reflexão das cônicas mas não sei como começar a questão.

A figura abaixo ilustra o exercício.

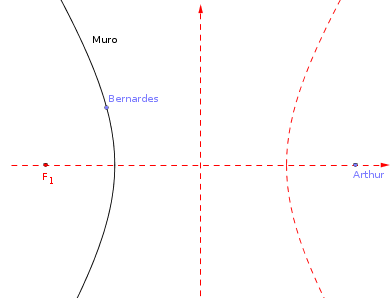
figura1.png (5.38 KiB) Exibido 1215 vezes

Se a bala tivesse atingido o muro como alega Arthur, note que considerando válida a propriedade de reflexão da hipérbole para a bala, então ela seria ricocheteada para longe de Bernardes. Vide a figura abaixo.

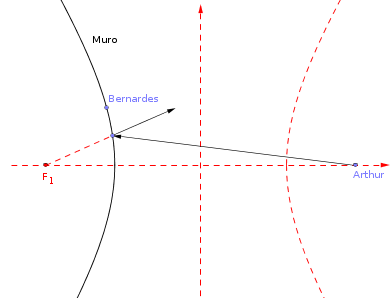
figura2.png (6.74 KiB) Exibido 1215 vezes

Agora tente concluir o exercício.