 por Joao » Qui Jul 23, 2009 18:32
por Joao » Qui Jul 23, 2009 18:32
Boa tarde!!!
Pessoal, o problema é o seguinte: O polinômio
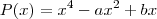
é divisível por x+3 e o resto de sua divisão por x-1 é a abcissa do ponto médio do segmento MN, onde M(-9,3) e N(-15,-4).Encontre os valores de a e b.
Bem, primeiro resolvi P(x) por x+3 pelo dispositivo de Briot-Ruffini e que deu um resultado nada satisfatório, então depois tirei a raiz de x+3=0 => x=-3
e fiz
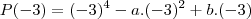
e cheguei a P(-3)= 81- 9a -3b. E daí em diante não consegui resolver o problema e nem aplicar os conceitos de geometria analítica.
Por favor, alguém me ajude nessa questão!!! 
-
Joao
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jul 23, 2009 16:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qui Jul 23, 2009 19:37
por Molina » Qui Jul 23, 2009 19:37
Boa noite, Joao.
Vamos por partes.
Primeiramente descobrir o ponto médio de M(-9,3) e N(-15,-4):
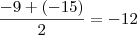
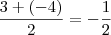 Ponto médio:
Ponto médio: (-12, -1/2)
Abscissa do ponto médio: -12
Ou seja, a divisão de
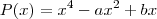
por

tem resto igual a
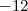
Tente a partir destas informações.
Use Briot-Ruffini que eu acho que vai dar certo.
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Joao » Sex Jul 24, 2009 16:34
por Joao » Sex Jul 24, 2009 16:34
Obrigado pela ajuda Molina!!!
Pois eu consegui terminar a resolução do problema.
É so que eu utilizei um método + prático do que o Dispositivo de Briot-Ruffini.
Bem, eu fiz assim:
Já que, x+3=0 => x=-3 e x-1=0=> x=1
Então:
P(x)=
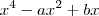
R(x)=P(1)= 1-a+b=-12
R(x)=P(-3)= 81-9a-3b=0
Logo,
{-a+b=-13.(3) (I)
{-9a-3b=-81
{-3a+3b=-39 (II)
{-9a-3b=-81
-12a= -120 => a=10 (III)
-10+b=-13 => b=-3
E bateu com gabarito, Vlw's!!!

-
Joao
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jul 23, 2009 16:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria plana] área e polinómios envolvidos
por fernandocez » Ter Nov 20, 2012 22:28
- 7 Respostas
- 7317 Exibições
- Última mensagem por fernandocez

Qua Nov 28, 2012 18:21
Geometria Plana
-
- [Geometria Espacial Polinômios] UESB 2011.2
por Leocondeuba » Ter Nov 05, 2013 22:08
- 1 Respostas
- 4204 Exibições
- Última mensagem por DanielFerreira

Dom Jan 31, 2016 21:33
Geometria Espacial
-
- Geometria Analítica
por maysa » Ter Abr 14, 2009 10:35
- 1 Respostas
- 7691 Exibições
- Última mensagem por Marcampucio

Ter Abr 14, 2009 15:52
Geometria Analítica
-
- GEOMETRIA ANALITICA
por GABRIELA » Ter Set 29, 2009 17:20
- 3 Respostas
- 5452 Exibições
- Última mensagem por GABRIELA

Qua Set 30, 2009 16:49
Geometria Analítica
-
- Geometria analítica
por shirata » Qua Nov 11, 2009 20:37
- 2 Respostas
- 4178 Exibições
- Última mensagem por shirata

Dom Nov 15, 2009 09:25
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
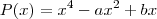 é divisível por x+3 e o resto de sua divisão por x-1 é a abcissa do ponto médio do segmento MN, onde M(-9,3) e N(-15,-4).Encontre os valores de a e b.
é divisível por x+3 e o resto de sua divisão por x-1 é a abcissa do ponto médio do segmento MN, onde M(-9,3) e N(-15,-4).Encontre os valores de a e b.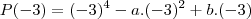 e cheguei a P(-3)= 81- 9a -3b. E daí em diante não consegui resolver o problema e nem aplicar os conceitos de geometria analítica.
e cheguei a P(-3)= 81- 9a -3b. E daí em diante não consegui resolver o problema e nem aplicar os conceitos de geometria analítica.


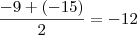
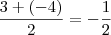
 tem resto igual a
tem resto igual a 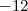


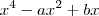
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.