 por Alyne_vieira » Qui Mai 17, 2012 20:30
por Alyne_vieira » Qui Mai 17, 2012 20:30
Meu professor passou um problema para resolver que ao você montar fica um sistema de 2 equações mas 3 incognitas!!! Tentei fazer Cramer, Escalonamento, O método da comparação, mas, não consegui resolver cheguei até a ficar com uma equação de 2 incognitas!!!
Cheguei a montar o sistema mas não consegui resolver meu sistema ficou assim:
3x+7y+z=42,1
4x+10y+z=47,3
Mas, não consegui resolver!!!
Problema:
Uma loja vende 3 tipos de lampadas (x,y,z. Tamara comprou 3 lampadas tipo x, 7 tipo y, e 1 tipo z, pagando R$42,10. José comprou 4 lampadas tipo x, 10 tipo y e uma tipo z, pagando R$47,30. Nas condições dadas, a compra de 3 lampadas, sendo uma de cada tipo custa:
a) R$ 30,50 b) R$ 31,40 c) R$ 31,70 d) 32,30 e)R$33,20
-
Alyne_vieira
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mai 17, 2012 20:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Mai 19, 2012 08:55
por DanielFerreira » Sáb Mai 19, 2012 08:55
Alyne,
seja bem vinda!
Vc montou o sistema corretamente. Agora, vamos isolar Z e ver no que dá.

============================>


===========================>

Podemos igualar certo?

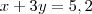
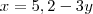
Se substituirmos este valor nas equações acima, veremos que aparecerá apenas uma equação. Podendo ter várias soluções.
Alyne,
quando estiver diante de um sistema cujo número de incógnitas é maior que o número de equações saiba que será indeterminado (diversas soluções).
Espero ter ajudado!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Alyne_vieira » Dom Mai 20, 2012 14:53
por Alyne_vieira » Dom Mai 20, 2012 14:53
Obrigada, pela ajuda!!!
-
Alyne_vieira
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mai 17, 2012 20:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Mai 20, 2012 17:21
por DanielFerreira » Dom Mai 20, 2012 17:21
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- problema de matematica
por verinha72 » Qua Out 06, 2010 23:24
- 1 Respostas
- 3486 Exibições
- Última mensagem por Elcioschin

Qui Out 07, 2010 17:57
Mensagens Matemáticas
-
- PROBLEMA DE MATEMÁTICA
por deiabae » Seg Ago 08, 2011 22:41
- 1 Respostas
- 2930 Exibições
- Última mensagem por Molina

Seg Ago 08, 2011 22:57
Funções
-
- problema de matematica
por orlene » Qui Set 15, 2011 13:43
- 1 Respostas
- 1840 Exibições
- Última mensagem por MarceloFantini

Qui Set 15, 2011 16:17
Matemática Financeira
-
- Problema de Matemática
por elmanoduarte » Qui Dez 01, 2011 10:29
- 1 Respostas
- 1580 Exibições
- Última mensagem por elmanoduarte

Qui Dez 01, 2011 20:57
Cálculo: Limites, Derivadas e Integrais
-
- problema de matemática 01
por leonardo151273 » Qua Mar 21, 2012 23:18
- 1 Respostas
- 1919 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 19, 2012 14:45
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ============================>
============================> 
 ===========================>
===========================> 

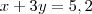
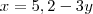




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.