 por Claudin » Dom Mai 13, 2012 14:34
por Claudin » Dom Mai 13, 2012 14:34
Determine a equação da elipse de focos (-3,0) e (3,0) e com eixo maior igual a 10.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por DanielFerreira » Sáb Mai 19, 2012 11:24
por DanielFerreira » Sáb Mai 19, 2012 11:24
Claudin escreveu:Determine a equação da elipse de focos (-3,0) e (3,0) e com eixo maior igual a 10.
Os focos (ponto) estão no eixo x, então podemos concluir que o eixo maior está em x;
Foco:

=============>


=============>

Eixo maior:

=============>

Eixo menor:
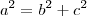
=====>

========>

Logo,
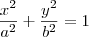

Se não errei nada é isso!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Claudin » Dom Mai 20, 2012 15:24
por Claudin » Dom Mai 20, 2012 15:24
Resultado que você obteve não condiz com o gabarito

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Dom Mai 20, 2012 15:26
por Claudin » Dom Mai 20, 2012 15:26
Aqui no gabarito a resposta é

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por DanielFerreira » Dom Mai 20, 2012 16:55
por DanielFerreira » Dom Mai 20, 2012 16:55
Tens razão,
vacilei feio!
danjr5 escreveu:Claudin escreveu:Determine a equação da elipse de focos (-3,0) e (3,0) e com eixo maior igual a 10.
Os focos (ponto) estão no eixo x, então podemos concluir que o eixo maior está em x;
Foco:

=============>


=============>

Eixo maior:

====== a = 5 =======>

Eixo menor:
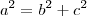
=====>

========>

Logo,
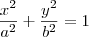

Desculpe o engano!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Claudin » Dom Mai 20, 2012 20:03
por Claudin » Dom Mai 20, 2012 20:03
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cônicas]Retas tangentes à cônicas
por Hopkins » Ter Fev 28, 2017 22:39
- 0 Respostas
- 1533 Exibições
- Última mensagem por Hopkins

Ter Fev 28, 2017 22:39
Geometria Analítica
-
- Conicas
por baianinha » Qua Set 14, 2011 00:30
- 1 Respostas
- 1440 Exibições
- Última mensagem por LuizAquino

Qua Set 14, 2011 00:58
Álgebra Elementar
-
- Cônicas
 por Claudin » Dom Mai 13, 2012 12:43
por Claudin » Dom Mai 13, 2012 12:43
- 7 Respostas
- 3152 Exibições
- Última mensagem por Claudin

Dom Mai 20, 2012 23:08
Geometria Analítica
-
- Cônicas
por Claudin » Dom Mai 13, 2012 14:35
- 7 Respostas
- 3028 Exibições
- Última mensagem por Claudin

Dom Mai 20, 2012 17:34
Geometria Analítica
-
- Cônicas
por Claudin » Dom Mai 13, 2012 14:37
- 3 Respostas
- 1537 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 19, 2012 10:16
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 =============>
=============> 
 =============>
=============> 
 =============>
=============> 
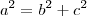 =====>
=====>  ========>
========> 
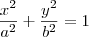






=============>
=============>
====== a = 5 =======>
=====>
========>



 .
.



