Estou com uma duvida:
Ha uma serie de Taylor que retorna o valor do arc tg(x) inserindo-se o x no somatorio. Porem, ela abrange apenas o intervalo de [-1,1], o que e insuficiente para a minha aplicacao. Gostaria de saber se ha alguma outra forma de se calcular (sem uso de calculadoras ou outros equipamentos, queria saber como se faz mesmo).
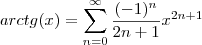
Para |x| < 1
Obrigado a todos que ajudarem.
Observacao: desculpem pela falta de acentuacao no texto.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)