Mateus Leao escreveu:O enunciado pede que seja calculado os pontos máximos (ou mínimos), de inflexão e assíntota.
A função é: y = 2x/x²+1
Consegui calcular o limite, sendo que há assíntota em x=0 na assíntota horizontal, mas não há no vertical.
Travei no cálculo do ponto máximo, mínimo e inflexão, visto que não tenho experiência no cálculo da 2 derivada com eficácia.
Primeiro, note que y = 2x/x² + 1 é equivalente a escrever:
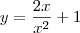
Entretanto, ao que parece você deseja:
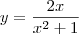
Nesse caso, você deveria ter escrito algo como y = 2x/(x² + 1). Note a importância do uso adequado dos parênteses!
Eu aproveito ainda para recomendar que você use o LaTeX em suas mensagens. Vide o tópico:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74Em relação ao exercício, antes de calcular a segunda derivada, você precisa calcular a primeira. Aplicando então a regra do quociente, você já deve saber que:
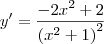
Aplicando novamente a regra do quociente, temos que:
![y^{\prime\prime} = \frac{\left(-2x^2 + 2\right)^\prime\left(x^2 + 1\right)^2 - \left(-2x^2 + 2\right)\left[\left(x^2 + 1\right)^2\right]^\prime}{\left[\left(x^2 + 1\right)^2\right]^2} y^{\prime\prime} = \frac{\left(-2x^2 + 2\right)^\prime\left(x^2 + 1\right)^2 - \left(-2x^2 + 2\right)\left[\left(x^2 + 1\right)^2\right]^\prime}{\left[\left(x^2 + 1\right)^2\right]^2}](/latexrender/pictures/63c00d26c565ec5bfb25f8338e5d65a6.png)
![y^{\prime\prime} = \frac{-4x\left(x^2 + 1\right)^2 - \left(-2x^2 + 2\right)\left[2\left(x^2 + 1\right)(2x)\right]}{\left(x^2 + 1\right)^4} y^{\prime\prime} = \frac{-4x\left(x^2 + 1\right)^2 - \left(-2x^2 + 2\right)\left[2\left(x^2 + 1\right)(2x)\right]}{\left(x^2 + 1\right)^4}](/latexrender/pictures/07d4627bb65272b47427f49b69644071.png)
Note que para calcular
![\left[\left(x^2 + 1\right)^2\right]^\prime \left[\left(x^2 + 1\right)^2\right]^\prime](/latexrender/pictures/4f08ae85b81c2558c323b4ae92fde901.png)
foi necessário aplicar a regra da cadeia.
Continuando a resolução, temos que:
![y^{\prime\prime} = \frac{-4x\left(x^2 + 1\right)^2 - \left[-2\left(x^2 - 1\right)\right]\left[4x\left(x^2 + 1\right)\right]}{\left(x^2 + 1\right)^4} y^{\prime\prime} = \frac{-4x\left(x^2 + 1\right)^2 - \left[-2\left(x^2 - 1\right)\right]\left[4x\left(x^2 + 1\right)\right]}{\left(x^2 + 1\right)^4}](/latexrender/pictures/cae0689fa8ccbadbb3e0af6abd8d6c01.png)
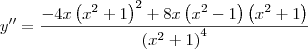
![y^{\prime\prime} = \frac{\left[-4x\left(x^2 + 1\right) + 8x\left(x^2 - 1\right)\right]\left(x^2 + 1\right)}{\left(x^2 + 1\right)^4} y^{\prime\prime} = \frac{\left[-4x\left(x^2 + 1\right) + 8x\left(x^2 - 1\right)\right]\left(x^2 + 1\right)}{\left(x^2 + 1\right)^4}](/latexrender/pictures/87513cca0f0ba0f26ca9f5226458a8c8.png)
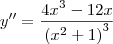
Agora tente continuar o exercício.


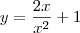
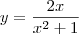
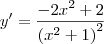
![y^{\prime\prime} = \frac{\left(-2x^2 + 2\right)^\prime\left(x^2 + 1\right)^2 - \left(-2x^2 + 2\right)\left[\left(x^2 + 1\right)^2\right]^\prime}{\left[\left(x^2 + 1\right)^2\right]^2} y^{\prime\prime} = \frac{\left(-2x^2 + 2\right)^\prime\left(x^2 + 1\right)^2 - \left(-2x^2 + 2\right)\left[\left(x^2 + 1\right)^2\right]^\prime}{\left[\left(x^2 + 1\right)^2\right]^2}](/latexrender/pictures/63c00d26c565ec5bfb25f8338e5d65a6.png)
![y^{\prime\prime} = \frac{-4x\left(x^2 + 1\right)^2 - \left(-2x^2 + 2\right)\left[2\left(x^2 + 1\right)(2x)\right]}{\left(x^2 + 1\right)^4} y^{\prime\prime} = \frac{-4x\left(x^2 + 1\right)^2 - \left(-2x^2 + 2\right)\left[2\left(x^2 + 1\right)(2x)\right]}{\left(x^2 + 1\right)^4}](/latexrender/pictures/07d4627bb65272b47427f49b69644071.png)
![\left[\left(x^2 + 1\right)^2\right]^\prime \left[\left(x^2 + 1\right)^2\right]^\prime](/latexrender/pictures/4f08ae85b81c2558c323b4ae92fde901.png) foi necessário aplicar a regra da cadeia.
foi necessário aplicar a regra da cadeia.![y^{\prime\prime} = \frac{-4x\left(x^2 + 1\right)^2 - \left[-2\left(x^2 - 1\right)\right]\left[4x\left(x^2 + 1\right)\right]}{\left(x^2 + 1\right)^4} y^{\prime\prime} = \frac{-4x\left(x^2 + 1\right)^2 - \left[-2\left(x^2 - 1\right)\right]\left[4x\left(x^2 + 1\right)\right]}{\left(x^2 + 1\right)^4}](/latexrender/pictures/cae0689fa8ccbadbb3e0af6abd8d6c01.png)
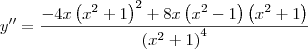
![y^{\prime\prime} = \frac{\left[-4x\left(x^2 + 1\right) + 8x\left(x^2 - 1\right)\right]\left(x^2 + 1\right)}{\left(x^2 + 1\right)^4} y^{\prime\prime} = \frac{\left[-4x\left(x^2 + 1\right) + 8x\left(x^2 - 1\right)\right]\left(x^2 + 1\right)}{\left(x^2 + 1\right)^4}](/latexrender/pictures/87513cca0f0ba0f26ca9f5226458a8c8.png)
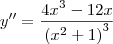


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.