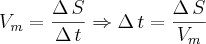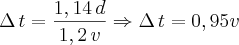por Alunos » Qua Mai 16, 2012 12:36
por Alunos » Qua Mai 16, 2012 12:36
Ao optar por um itinerario 14% mais longo, um motorista acha que podera ganhar tempo, pois, por ser o trafego melhor, podera aumetar sua velocidade em 20%. Entao, o tempo de viagem diminuira em:
(O gabarito é 5%)
Gostaria de saber quais são os critérios basicos para resolver os diversos tipos de problemas de porcentagem, de uma forma mais rápida e simples.
-
Alunos
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Mai 16, 2012 01:46
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Qua Mai 16, 2012 15:03
por Cleyson007 » Qua Mai 16, 2012 15:03
Boa tarde Alunos!
Sejam: d= distância normal (original)
d
a= distância alterada (aumentando o itinerário) = 1,14d
v = velocidade executada pelo motorista
v
a=aumento da velocidade = 1,2v
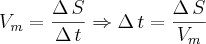
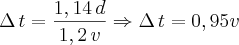
Repare que houve uma diminuição do tempo de t para 0,95t --> 5%
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão UFMG
por Guilherme Carvalho » Qui Mar 03, 2011 13:03
- 1 Respostas
- 4778 Exibições
- Última mensagem por Elcioschin

Qui Mar 03, 2011 13:27
Álgebra Elementar
-
- Questão da UFMG
por Kelvin Brayan » Sáb Mar 12, 2011 17:19
- 1 Respostas
- 5011 Exibições
- Última mensagem por Rogerio Murcila

Qua Mar 16, 2011 23:42
Matemática Financeira
-
- Questão da UFMG
por Kelvin Brayan » Dom Mar 13, 2011 16:26
- 4 Respostas
- 2644 Exibições
- Última mensagem por Kelvin Brayan

Seg Mar 14, 2011 00:34
Cálculo: Limites, Derivadas e Integrais
-
- Questão UFMG
por Guilherme Carvalho » Qua Mar 16, 2011 16:39
- 5 Respostas
- 3061 Exibições
- Última mensagem por Kelvin Brayan

Ter Mar 22, 2011 00:23
Funções
-
- Questão UFMG
por Kelvin Brayan » Dom Mar 27, 2011 13:36
- 2 Respostas
- 4706 Exibições
- Última mensagem por Kelvin Brayan

Dom Mar 27, 2011 14:15
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.