Ana_Rodrigues escreveu:Um farol giratório completa uma volta a cada 15 segundos. O farol está a 60m de P, o ponto mais próximo em uma praia retilínea. Determine a razão em que um raio de luz do farol está se movendo ao longo da praia em um ponto, Q, a 150m de P.
Resposta:
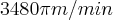
Ana_Rodrigues escreveu:Eu não estou conseguindo achar uma equação que relacione o ponto P e Q. Primeiro eu pensei na seguinte situação
O farol seria o centro das circunferências que passam pelos pontos P e Q e pensei nos pontos P, Q e o farol como pontos colineares, daí seria fácil achar o raio da circunferência que passa por Q, mas não necessariamente isso tem que ocorrer. Daí o máximo que consegui fazer foi achar a taxa de variação de P que é:
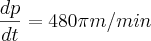
Como posso achar uma equação que relacione P e Q?
Note que P, Q e F não são colineares. Além disso, essa taxa de variação que você determinou não faz sentido.
Vejamos o início da resolução.
A figura abaixo ilustra o exercício.
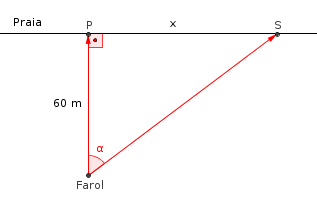
- figura.png (11.64 KiB) Exibido 5426 vezes
Deseja-se saber o que acontece quando x = 150 m. Nesse caso, teremos S = Q.
Como o farol dá 1 volta completa a cada 15 segundos, temos que a taxa de variação do ângulo

em relação ao tempo é igual a
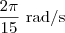
. Em outras palavras, temos que
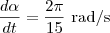
.
Analisando o triângulo retângulo ilustrado na figura, temos que:

Sendo assim, temos que:
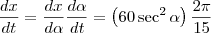
Quando x = 150 m, no triângulo retângulo temos que:
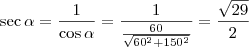
Agora tente continuar o exercício a partir daí.
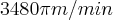
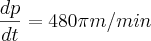


 em relação ao tempo é igual a
em relação ao tempo é igual a 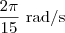 . Em outras palavras, temos que
. Em outras palavras, temos que 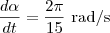 .
.
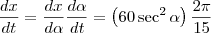
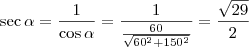


 .
.
 :
: