A área da região do primeiro quadrante delimitada pelas retas que são soluções da equação cos(x+y)=0, com
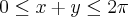 , é igual a:
, é igual a:Resposta:
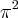 unidades de área
unidades de áreaEu cheguei a:
cos x . cos y - sen x . sen y = 0
cos x . cos y = sen x . sen y
tg y . tg x = 1
Daí fui analisando as possibilidades e obtive como possíveis:

Daí tracei as retas no círculo trigonométrico (só tracei as que cortam o primeiro quadrante), mas nas minhas tentativas de calcular a área não cheguei nenhuma vez a
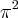 , porque parti de que a área da circunferência é
, porque parti de que a área da circunferência é  .
.Como prossigo se é que está certo?
Grata desde já!


 logo pensamos em desenvolver a soma de arcos.
logo pensamos em desenvolver a soma de arcos. inteiro.
inteiro.

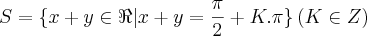
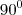
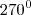
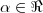 ,
, 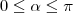 ,
, 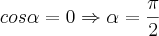
 real,
real, ![\alpha \in [0, \pi] \alpha \in [0, \pi]](/latexrender/pictures/0842c803519eb6c851b3f39181776d01.png) ,
,  ou
ou  , ótimo!
, ótimo!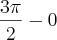

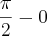
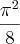
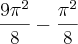
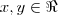 , o primeiro quadrante é a intersecção das regiões representadas por estas inequações:
, o primeiro quadrante é a intersecção das regiões representadas por estas inequações:
 .
. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.