Feita uma pesquisa em determinada escola sobre a preferência dos alunos por esporte obteve-se o seguinte
resultado.
60% dos alunos gostam de dança.
55% dos alunos gostam de ginástica.
10% dos alunos não gostam nem de dança nem de ginástica.
50 pessoas gostam tanto de dança quanto de ginástica.
Com os dados acima podemos afirmar que foram entrevistados um total de:
A) 100 alunos D) 200 alunos
B) 150 alunos E) 300 alunos
C) 500 alunos
Gostaria de ver a resolução dessa questão!!
Por favor!!!



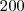 , mas gostaria de saber, porque temos que descontar o número de alunos que gostam tanto de dança como de ginástica!
, mas gostaria de saber, porque temos que descontar o número de alunos que gostam tanto de dança como de ginástica!

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)