 por FernandoCHT » Qua Mai 09, 2012 21:22
por FernandoCHT » Qua Mai 09, 2012 21:22
Boa noite pessoal,sou novo no forum,pois estou aqui tentando fazer umas questões muito cabulosas.Estou tentando a 3 dias,mas não vou desistir.
Bom,gostaria se for possivel da ajuda de vcs.Pois esse trabalho vale a minha nota trimestral.
Claro o meu objetivo é aprender,mas poderião me ajudar?
obrigado,muito obrigado
abraços.
1) Determine os numeros complexos Z1 e Z2 tais que
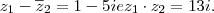
Desculpe se não postei certo.
Editado pela última vez por
FernandoCHT em Qua Mai 09, 2012 22:31, em um total de 5 vezes.
-
FernandoCHT
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Mai 09, 2012 21:18
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por MarceloFantini » Qua Mai 09, 2012 21:32
por MarceloFantini » Qua Mai 09, 2012 21:32
Bem vindo ao fórum Fernando. Leia as regras do fórum: poste apenas uma questão por tópico, digite o enunciado e utilize figuras apenas se estritamente necessário, usando LaTeX para redigir as equações.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por joaofonseca » Qua Mai 09, 2012 22:11
por joaofonseca » Qua Mai 09, 2012 22:11
Será que vocês escreveu isto:
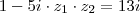
?
Para dois números complexos serem iguais as partes reais e imaginarias devem ser iguais.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por FernandoCHT » Qua Mai 09, 2012 22:19
por FernandoCHT » Qua Mai 09, 2012 22:19
joaofonseca escreveu:Será que vocês escreveu isto:
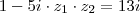
?
Para dois números complexos serem iguais as partes reais e imaginarias devem ser iguais.
Na verdade está na folha assim {Z1 - Z2(conjugado)=1-5i
Em baixo disso está:::::::::::::::Z1 x Z2 = - 13 i
Me desculpa por não conseguir com a tex.
Poderia postar a imagem só para vcs visualizarem?
obrigado pela paciencia.
-
FernandoCHT
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Mai 09, 2012 21:18
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por MarceloFantini » Qua Mai 09, 2012 22:20
por MarceloFantini » Qua Mai 09, 2012 22:20
Na verdade as equações são

e
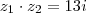
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por FernandoCHT » Qua Mai 09, 2012 22:24
por FernandoCHT » Qua Mai 09, 2012 22:24
MarceloFantini escreveu:Na verdade as equações são

e
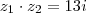
.
Isso Marcelo,muito obrigado.Desculpe pela bagunça.
-
FernandoCHT
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Mai 09, 2012 21:18
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por MarceloFantini » Qua Mai 09, 2012 22:39
por MarceloFantini » Qua Mai 09, 2012 22:39
Agora, quais foram suas tentativas?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por FernandoCHT » Qua Mai 09, 2012 22:45
por FernandoCHT » Qua Mai 09, 2012 22:45
FernandoCHT escreveu:MarceloFantini escreveu:Na verdade as equações são

e
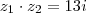
.
Isso Marcelo,muito obrigado.Desculpe pela bagunça.
Substituir o z por A+bi e o Z2 por C+Di,troquei o sinal por causa da conjução e igualei a 1-5i.na parte de multiplicação foi feito a mesmo procedimento,multiplicando e igualando a -13i.Depois separei os números reais dos imaginários chegando ao resultado:
Subtração da primeira parte do sistema= A-C=1 e B+D=5i
Multiplicação=AC-BD=0 e AD + BC = -13i
E apartir daqui não sai mais nada.
-
FernandoCHT
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Mai 09, 2012 21:18
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17117 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- Duas questões de complexos
por Joseaugusto » Seg Abr 09, 2012 10:43
- 3 Respostas
- 3904 Exibições
- Última mensagem por fraol

Ter Abr 10, 2012 10:35
Números Complexos
-
- Numeros complexos!
por Estela » Seg Mar 17, 2008 00:57
- 7 Respostas
- 13360 Exibições
- Última mensagem por andegledson

Seg Nov 02, 2009 21:41
Números Complexos
-
- Números Complexos
por michelle » Dom Ago 31, 2008 15:35
- 3 Respostas
- 10335 Exibições
- Última mensagem por admin

Dom Ago 31, 2008 21:00
Números Complexos
-
- Números Complexos
por Cleyson007 » Qui Mai 14, 2009 13:57
- 7 Respostas
- 13963 Exibições
- Última mensagem por Cleyson007

Sáb Mai 16, 2009 11:04
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
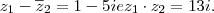




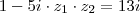 ?
?
 e
e 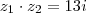 .
.




