 por Pri Ferreira » Ter Mai 08, 2012 20:42
por Pri Ferreira » Ter Mai 08, 2012 20:42
Uma urna contém exatamente sete bolas: quatro azuis (A) e três vermelhas (V). Retira-se, ao acaso, uma bola da
urna, registra-se sua cor e repõe-se a bola na urna. A seguir, retira-se novamente ao acaso, uma bola da urna e
registra-se sua cor. Então, a probabilidade de saírem duas bolas de cores diferentes será igual a:
Por favor, ajudem!!!
-
Pri Ferreira
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Qua Out 19, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por Fabiano Vieira » Qua Mai 09, 2012 20:37
por Fabiano Vieira » Qua Mai 09, 2012 20:37
.
Editado pela última vez por
Fabiano Vieira em Qua Mai 09, 2012 22:31, em um total de 1 vez.
-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
 por joaofonseca » Qua Mai 09, 2012 21:04
por joaofonseca » Qua Mai 09, 2012 21:04
Julgo que se deve multiplicar as probabilidades "elementares" e não soma-las. Pois se a 1ª bola é Azul e a 2ª bola é Vermelha, temos:
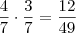
Mas a ordem pode ser inversa.
Ter AZUL-VERMELHO é diferente de ter VERMEHO-AZUL.Pois são resultados possíveis. Assim a probabilidade encontrada deve ser multiplicada por 2.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Fabiano Vieira » Qua Mai 09, 2012 21:27
por Fabiano Vieira » Qua Mai 09, 2012 21:27
.
-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Urna
por Rafael16 » Seg Dez 10, 2012 21:46
- 3 Respostas
- 4724 Exibições
- Última mensagem por young_jedi

Seg Dez 10, 2012 22:30
Análise Combinatória
-
- [Probabilidade]Em uma urna existem ........
por daniloktt » Ter Abr 24, 2012 02:12
- 0 Respostas
- 1096 Exibições
- Última mensagem por daniloktt

Ter Abr 24, 2012 02:12
Probabilidade
-
- Questão de concurso...
por henrivoador » Seg Abr 19, 2010 20:37
- 7 Respostas
- 11306 Exibições
- Última mensagem por henrivoador

Seg Abr 26, 2010 13:07
Logaritmos
-
- Questão de concurso
por bia rosendo » Qua Fev 23, 2011 11:00
- 4 Respostas
- 5814 Exibições
- Última mensagem por Elcioschin

Qui Fev 24, 2011 11:08
Funções
-
- Questão de concurso
 por bia rosendo » Seg Fev 28, 2011 22:54
por bia rosendo » Seg Fev 28, 2011 22:54
- 2 Respostas
- 7744 Exibições
- Última mensagem por LuizAquino

Ter Mar 01, 2011 14:12
Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


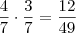

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
