 por carcleo » Ter Mai 08, 2012 10:02
por carcleo » Ter Mai 08, 2012 10:02
Como resolver essa equação?

Obrigado a quem puder ajudar!
Carlos Rocha
-
carcleo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Nov 16, 2011 07:35
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Contabilidade
- Andamento: formado
 por Cleyson007 » Ter Mai 08, 2012 10:50
por Cleyson007 » Ter Mai 08, 2012 10:50
Bom dia Carlos Rocha!
Carlos, experimente passar o (x+3) para o lado direito da igualdade. Você chegará nessa equação x(5x²-9x-2)=0.
Tente resolver a partir daí e comente qualquer dúvida

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por carcleo » Ter Mai 08, 2012 12:14
por carcleo » Ter Mai 08, 2012 12:14
Pelo que entendi, se passar o x-3 para outro lado ele vai dividir o 0 e ai vai dar dar 0 e então terei só a primeira expressão.
É isso mesmo?
Mas não consigo continuar.
Tô cru mesmo.
Se puder ajudar mai uma etapa, talves consiga terminar.
-
carcleo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Nov 16, 2011 07:35
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Contabilidade
- Andamento: formado
 por Russman » Ter Mai 08, 2012 14:34
por Russman » Ter Mai 08, 2012 14:34
Sempre nestas situações tente fatorar ao máximo a equação. isto é, transformá-la de uma soma em um produto de alguns fatores pois assim você pode tomar cada um deles igual a zero!
Veja que a equação

tem uma raíz

pois tomamos o segundo fator

igual a zero.
Agora o outro fator

pode ainda ser fatorado para
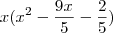
. Assim, tomamos

e
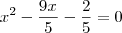
.
Assim, as outras 3 raízes são
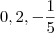
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por carcleo » Ter Mai 08, 2012 15:34
por carcleo » Ter Mai 08, 2012 15:34
Acho que entendi.
Então você quer dizer que a solução dessa equação:

é determinar as raizes da Equação que no caso são três: -3; 0,2; -1/5.
É isso mesmo?
-
carcleo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Nov 16, 2011 07:35
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Contabilidade
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8720 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
-
- Como resolver essa equação?
por viniciusantonio » Qua Out 21, 2009 19:17
- 1 Respostas
- 4157 Exibições
- Última mensagem por carlos r m oliveira

Qui Out 22, 2009 14:55
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver a equação linear?
por btag » Qui Mai 05, 2011 14:33
- 1 Respostas
- 1703 Exibições
- Última mensagem por carlosalesouza

Qui Mai 05, 2011 15:39
Sistemas de Equações
-
- Equação de Matrizes - Como Resolver
por juniocs » Qua Set 19, 2012 09:44
- 11 Respostas
- 6563 Exibições
- Última mensagem por Cleyson007

Qua Set 19, 2012 17:10
Álgebra Linear
-
- [Equação Trigonométrica]Como resolver
por mthc10 » Sáb Out 05, 2013 00:15
- 4 Respostas
- 2158 Exibições
- Última mensagem por mthc10

Dom Out 06, 2013 22:40
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







 tem uma raíz
tem uma raíz  pois tomamos o segundo fator
pois tomamos o segundo fator  igual a zero.
igual a zero. pode ainda ser fatorado para
pode ainda ser fatorado para 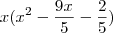 . Assim, tomamos
. Assim, tomamos
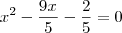 .
.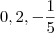 .
.



 .
.



