

fixe um elemento do conjunto e conte o total de subconjuntos de tamanho k que contem o elemento e o total de subconjuntos de tamnho k que nao o contem.





Aparecida escreveu:1. Um lote contém 12 itens bons e 8 itens defeituosos. Uma amostra de 5 itens é extraída. Determine o total de amostras contendo exatamente 3 itens bons.
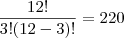
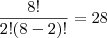



psdias escreveu:Olá, Fabiano !
Fiz as mesmas contas que você, chegando a 220 e 28, mas
eu MULTIPLIQUEI esses valores, chegando a 6.160.
Não entendi porque você somou os dois resultados. Pode explicar, por favor ?

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)