 por Russman » Sex Mai 04, 2012 01:13
por Russman » Sex Mai 04, 2012 01:13
Seja
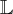
o operador Transformada de Laplace, isto é,
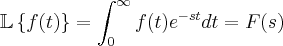
.
Gostaria de obter uma identidade para a seguinte Transformada:
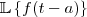
. Isto é, qual a relação da transformada da
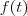
para com a mesma função mas linearmente deslocada?
Eu conheço a propriedade
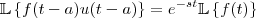
, onde
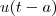
é a Função de Heaviside.
Mas e se a função
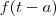
não estiver multiplicada por
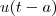
?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por LuizAquino » Sex Mai 04, 2012 11:35
por LuizAquino » Sex Mai 04, 2012 11:35
Russman escreveu:Seja
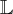
o operador Transformada de Laplace, isto é,
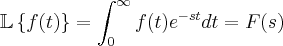
.
Gostaria de obter uma identidade para a seguinte Transformada:
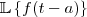
. Isto é, qual a relação da transformada da
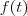
para com a mesma função mas linearmente deslocada?
Eu conheço a propriedade
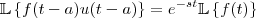
, onde
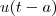
é a Função de Heaviside.
Mas e se a função
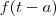
não estiver multiplicada por
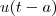
?
Basta calcular a transformada de Laplace para f(t - a). Vide, por exemplo, a página abaixo.
Teoremas simples da Transformada de Laplacehttp://w3.ualg.pt/~sjesus/aulas/ac/node32.html
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por pvgomes07 » Sex Ago 10, 2012 13:11
por pvgomes07 » Sex Ago 10, 2012 13:11
Só você usar a definição da Transformada e substituir
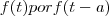
.
Lembrando que os limites de integração vão de
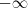
a
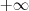
Aí você faz uma substituição no argumento de
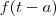
:
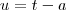
logo
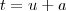
, onde vc vai substituir no expoente do termo
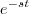
:
que vai ficar
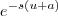
Separa em dois termos exponenciais e tira o
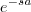
da integral.
A única diferença é que a integração vai ser de
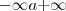
.
Ou seja, é uma transformada bilateral.. :S
-
pvgomes07
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Ago 05, 2012 17:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [TRANSFORMADA DE LAPLACE]
 por liviabgomes » Qui Dez 01, 2011 15:19
por liviabgomes » Qui Dez 01, 2011 15:19
- 1 Respostas
- 1223 Exibições
- Última mensagem por LuizAquino

Seg Dez 05, 2011 10:19
Cálculo: Limites, Derivadas e Integrais
-
- transformada de laplace
por theSinister » Seg Nov 05, 2012 16:01
- 2 Respostas
- 1254 Exibições
- Última mensagem por theSinister

Seg Nov 05, 2012 18:11
Cálculo: Limites, Derivadas e Integrais
-
- [Transformada de laplace] de funções
por jeferson_justo135 » Seg Jan 12, 2015 22:48
- 7 Respostas
- 3860 Exibições
- Última mensagem por jeferson_justo135

Dom Fev 08, 2015 16:53
Cálculo: Limites, Derivadas e Integrais
-
- Transformada de Laplace - função de transferência
por pvgomes07 » Sex Ago 10, 2012 12:52
- 2 Respostas
- 1613 Exibições
- Última mensagem por pvgomes07

Qui Ago 16, 2012 15:40
Cálculo: Limites, Derivadas e Integrais
-
- coordenadas esfericas Laplace tridimensional
por rhuam » Sex Set 15, 2017 09:36
- 0 Respostas
- 1834 Exibições
- Última mensagem por rhuam

Sex Set 15, 2017 09:36
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
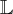 o operador Transformada de Laplace, isto é,
o operador Transformada de Laplace, isto é, 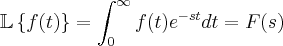 .
.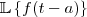 . Isto é, qual a relação da transformada da
. Isto é, qual a relação da transformada da 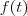 para com a mesma função mas linearmente deslocada?
para com a mesma função mas linearmente deslocada?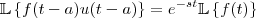 , onde
, onde 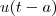 é a Função de Heaviside.
é a Função de Heaviside.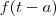 não estiver multiplicada por
não estiver multiplicada por 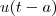 ?
?


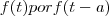 .
.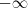 a
a 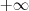
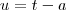
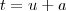 , onde vc vai substituir no expoente do termo
, onde vc vai substituir no expoente do termo 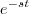 :
: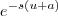
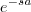 da integral.
da integral.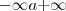 .
. 


 , avisa que eu resolvo.
, avisa que eu resolvo.

