 por carolina camargo » Ter Jul 07, 2009 19:08
por carolina camargo » Ter Jul 07, 2009 19:08
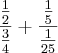
Como fazer essa divisão de fração?
Eu cheguei em:
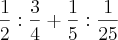
Invertendo a segunda fração de cada divisão eu não consegui chegar ao resultado que é 17/3.
Se alguém puder me ajudar, tenho problemas em matemática básica.
Valeuu!
-
carolina camargo
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jun 16, 2009 16:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por lucasguedes » Ter Jul 07, 2009 20:12
por lucasguedes » Ter Jul 07, 2009 20:12
carolina camargo escreveu: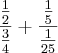
Como fazer essa divisão de fração?
Eu cheguei em:
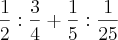
Invertendo a segunda fração de cada divisão eu não consegui chegar ao resultado que é 17/3.
Se alguém puder me ajudar, tenho problemas em matemática básica.
Valeuu!
na divisão de fração, pegamos a primeira fração e multiplicamos pelo inverso da segunda! veja:
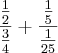
pegando as de cima e multiplicando pelo inverso da de baixo obteremos o seguinte:

.

=


.
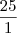
=

Somando-se o 5 com a fração 2/3, para somarmos multiplicamos o 5 pelo denominador 3 e somamos com o numerador 2 e repetimos a base q é o denominador 3. Ou seja, teremos 5 +

=
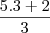
=
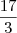
-
lucasguedes
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Jun 25, 2009 19:12
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: curso tecnico em eletrotecnica
- Andamento: cursando
 por Cleyson007 » Qua Jul 08, 2009 17:55
por Cleyson007 » Qua Jul 08, 2009 17:55
Boa tarde Carolina Carmargo!
Resolve-se assim:
Da primeira divisão de frações:
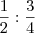
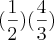
-->

Da segunda divisão de frações:
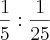
-->
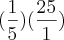
Como pede a soma do resultado das duas divisões:

Tirando o mmc -->
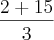
Logo, o resultado é:
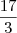
Comente qualquer dúvida,

?
Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por carolina camargo » Qua Jul 08, 2009 19:00
por carolina camargo » Qua Jul 08, 2009 19:00
Ficou bem claro pra mim, obrigadíssima!
-
carolina camargo
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jun 16, 2009 16:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Divisão de frações
por AG3 » Sáb Out 03, 2009 01:51
- 1 Respostas
- 1462 Exibições
- Última mensagem por Cleyson007

Sáb Out 03, 2009 13:30
Cálculo: Limites, Derivadas e Integrais
-
- Divisão de frações
por eliky » Sex Jan 18, 2013 20:26
- 4 Respostas
- 1783 Exibições
- Última mensagem por eliky

Sex Jan 18, 2013 22:05
Álgebra Elementar
-
- [Frações] Regra de frações
por raymondtfr » Dom Nov 02, 2014 16:49
- 4 Respostas
- 3326 Exibições
- Última mensagem por Russman

Dom Nov 02, 2014 23:57
Aritmética
-
- FRAÇÕES
por csantos » Sex Ago 29, 2008 16:33
- 1 Respostas
- 3265 Exibições
- Última mensagem por admin

Sex Ago 29, 2008 16:47
Álgebra Elementar
-
- frações
por suryah » Qua Out 20, 2010 18:28
- 3 Respostas
- 3580 Exibições
- Última mensagem por DanielFerreira

Seg Nov 29, 2010 19:54
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
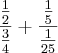 Como fazer essa divisão de fração?
Como fazer essa divisão de fração?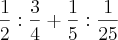

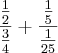 Como fazer essa divisão de fração?
Como fazer essa divisão de fração?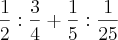

Como fazer essa divisão de fração?
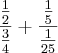
 .
.  =
= 
 .
. 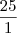 =
= 
 =
= 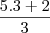 =
= 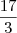

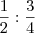
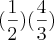 -->
--> 
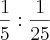 -->
--> 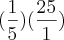

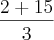
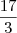
 ?
?


 .
.



