 por cjunior94 » Seg Abr 30, 2012 17:55
por cjunior94 » Seg Abr 30, 2012 17:55
Bom dia,
gostaria de pedir ajuda nesse limite que não consegui resolver:
![\lim_{x\rightarrow\infty} \frac{lnx}{\sqrt[]{x}} \lim_{x\rightarrow\infty} \frac{lnx}{\sqrt[]{x}}](/latexrender/pictures/da6ad8eeed68719f072612d87ee8a0e0.png)
desde já, obrigado!
-
cjunior94
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mar 18, 2012 11:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por cjunior94 » Seg Abr 30, 2012 22:30
por cjunior94 » Seg Abr 30, 2012 22:30
Muito obrigado, Guill!
Havia chegado em:
![\lim_{x\rightarrow\infty} \frac{2.\sqrt[]{x}}{x} \lim_{x\rightarrow\infty} \frac{2.\sqrt[]{x}}{x}](/latexrender/pictures/40a37d3641e35c67b4cdae73c5287a31.png)
mas não pensei em dividir tudo por raiz de x para chegar no resultado:
![\lim_{x\rightarrow\infty} \frac{2}{\sqrt[]{x}} = 0 \lim_{x\rightarrow\infty} \frac{2}{\sqrt[]{x}} = 0](/latexrender/pictures/d2f5605b3db13981a5a3490aca9e9b2e.png)
[/quote]
vlws mesmo!
-
cjunior94
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mar 18, 2012 11:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Guill » Seg Abr 30, 2012 23:58
por Guill » Seg Abr 30, 2012 23:58
De fato.
Editado pela última vez por
Guill em Qua Mai 02, 2012 20:46, em um total de 1 vez.
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Ter Mai 01, 2012 17:47
por fraol » Ter Mai 01, 2012 17:47
Boa tarde,
Guill, estava estudando essa sua solução e encontrei uma inconsistência.Corrija-me se for o caso:
Guill escreveu:A partir de x = 1, a fração do numerador garante que a função f(x) nunca será menor do que a função . Portanto é possível afirmar que:
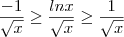
Um número negativo não é maior do que um número positivo e a relação proposta não vale sempre.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite indeterminado
por ewald » Qui Mai 05, 2011 17:55
- 1 Respostas
- 1854 Exibições
- Última mensagem por LuizAquino

Qui Mai 05, 2011 18:12
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminado 0/0
por ewald » Qui Mai 05, 2011 19:08
- 1 Respostas
- 4369 Exibições
- Última mensagem por LuizAquino

Qui Mai 05, 2011 19:41
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminado
por ewald » Ter Mai 17, 2011 15:40
- 13 Respostas
- 6675 Exibições
- Última mensagem por FilipeCaceres

Qua Mai 18, 2011 15:47
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminado ? - ?
por cjunior94 » Ter Mai 01, 2012 22:00
- 1 Respostas
- 1880 Exibições
- Última mensagem por LuizAquino

Qua Mai 02, 2012 14:17
Cálculo: Limites, Derivadas e Integrais
-
- Duvida limite indeterminado
por ewald » Seg Mai 09, 2011 17:20
- 1 Respostas
- 2553 Exibições
- Última mensagem por LuizAquino

Seg Mai 09, 2011 20:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow\infty} \frac{lnx}{\sqrt[]{x}} \lim_{x\rightarrow\infty} \frac{lnx}{\sqrt[]{x}}](/latexrender/pictures/da6ad8eeed68719f072612d87ee8a0e0.png)

![\lim_{x\rightarrow\infty} \frac{lnx}{\sqrt[]{x}} \lim_{x\rightarrow\infty} \frac{lnx}{\sqrt[]{x}}](/latexrender/pictures/da6ad8eeed68719f072612d87ee8a0e0.png)

![\lim_{x\rightarrow\infty} \frac{lnx}{\sqrt[]{x}} \lim_{x\rightarrow\infty} \frac{lnx}{\sqrt[]{x}}](/latexrender/pictures/da6ad8eeed68719f072612d87ee8a0e0.png)
![\lim_{x\rightarrow\infty} \frac{\frac{1}{x}}{\frac{1}{2\sqrt[]{x}}} \lim_{x\rightarrow\infty} \frac{\frac{1}{x}}{\frac{1}{2\sqrt[]{x}}}](/latexrender/pictures/c59c8ad4c4e595a7116b0b1432e4ddcb.png)
![\lim_{x\rightarrow\infty} \frac{2.\sqrt[]{x}}{x} \lim_{x\rightarrow\infty} \frac{2.\sqrt[]{x}}{x}](/latexrender/pictures/40a37d3641e35c67b4cdae73c5287a31.png)
![\lim_{x\rightarrow\infty} \frac{2}{\sqrt[]{x}} = 0 \lim_{x\rightarrow\infty} \frac{2}{\sqrt[]{x}} = 0](/latexrender/pictures/d2f5605b3db13981a5a3490aca9e9b2e.png)

![\lim_{x\rightarrow\infty} \frac{2.\sqrt[]{x}}{x} \lim_{x\rightarrow\infty} \frac{2.\sqrt[]{x}}{x}](/latexrender/pictures/40a37d3641e35c67b4cdae73c5287a31.png)
![\lim_{x\rightarrow\infty} \frac{2}{\sqrt[]{x}} = 0 \lim_{x\rightarrow\infty} \frac{2}{\sqrt[]{x}} = 0](/latexrender/pictures/d2f5605b3db13981a5a3490aca9e9b2e.png) [/quote]
[/quote]

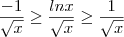


 .
.



