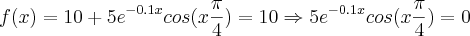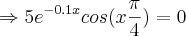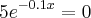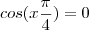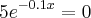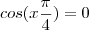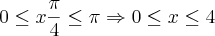por anamendes » Seg Abr 30, 2012 17:06
por anamendes » Seg Abr 30, 2012 17:06
como resolvo esta equação?
f(x)=10+5e^(-0.1x) cos??x/4?= 10
-
anamendes
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sáb Abr 28, 2012 08:01
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ciências e tecnologias
- Andamento: cursando
 por nakagumahissao » Seg Abr 30, 2012 20:22
por nakagumahissao » Seg Abr 30, 2012 20:22
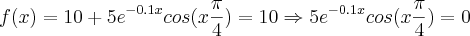
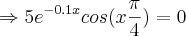
Temos duas possibilidades à partir daí, quais sejam:
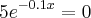
ou
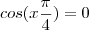
Sabemos que:
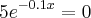
é sempre diferente de zero e portanto a igualdade não se comprovará nunca. Por um outro lado,
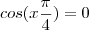
x = 0 ou x = 4
que são as soluções do problema. De fato, substituindo esses valores um à um na equação inicial, a igualdade é satisfeita, lembrando que estamos considerando o intervalo:
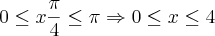
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por anamendes » Ter Mai 01, 2012 07:46
por anamendes » Ter Mai 01, 2012 07:46
ah muito obrigada!
já agora, como resolvo esta ?
sen(2x)=cos(2x - 5pi/6) ??

-
anamendes
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sáb Abr 28, 2012 08:01
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ciências e tecnologias
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7735 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13238 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13030 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6098 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8720 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.