 por jemourafer » Sáb Abr 28, 2012 00:18
por jemourafer » Sáb Abr 28, 2012 00:18
Estava fazendo uma lista de cálculo I-A e me deparei com essas duas questões parecidas, porém intrigantes. Os enunciados das questões são o seguinte:
1) Seja

, se x<1; e
![f(x)=\frac{1}{\sqrt[]{x}} f(x)=\frac{1}{\sqrt[]{x}}](/latexrender/pictures/7bf247bc7b411982b7b188fef14e9a7b.png)
, se x

1; a)f é diferenciável em x=1? b)f é contínua em x=1?
Resposta do gabarito: f é diferenciável em x=1 pois f'(1)=-1/2; f é contínua em x=1, pois tem um teorema que garante que toda função diferenciável num ponto é contínua nesse ponto.
2)Seja

, se x<1; e
![f(x)=\frac{1}{\sqrt[]{x}} f(x)=\frac{1}{\sqrt[]{x}}](/latexrender/pictures/7bf247bc7b411982b7b188fef14e9a7b.png)
, se x

1; a)f é diferenciável em x=1? b)f é contínua em x=1?
Resposta do gabarito:f não é contínua em x=1, pois

; f não é diferenciável em x=1 pois se fosse, f seria contínua em x=1.
Minha resolução: Na 1ª questão resolvi dessa forma: A função f é diferenciável em x=1 somente se

existir.
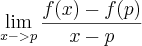
=

:.
![\lim_{x->1+}\frac{\frac{1}{\sqrt[]{x}}-\frac{1}{\sqrt[]{1}}}{x-1}=-\frac{1}{2} \lim_{x->1+}\frac{\frac{1}{\sqrt[]{x}}-\frac{1}{\sqrt[]{1}}}{x-1}=-\frac{1}{2}](/latexrender/pictures/604fef5bfae41462756f094dd03883e6.png)
. Como

, concluímos que o limite bilateral existe e então podemos dizer que f(x) é derivável em x=1. A função também é contínua em x=1, pois é derivável nesse ponto. Essa minha resposta está de acordo com o gabarito!
Já a 2ª questão, tentei fazer da mesma forma e deu que

(que está de acordo com o gabarito), mas quando

deveria valer -1/2 como na questão anterior, no gabarito diz que vale 1. No que eu errei?
-
jemourafer
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Abr 01, 2012 20:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por MarceloFantini » Dom Abr 29, 2012 15:28
por MarceloFantini » Dom Abr 29, 2012 15:28
Note que para
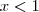
temos que

, enquanto que para
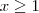
temos

. Calculando os limites laterais, vemos

e

. Como coincidem, o limite existe e a função é diferenciável no ponto, portanto contínua.
Seu entendimento está incorreto. A função pode ser contínua sem ser diferenciável, como no caso

na origem, ou de forma mais extrema procure sobre a
função de Weierstrass.
Agora, o teorema afirma que
se uma função é diferenciável num ponto, então ela é contínua neste ponto. A
contrapositiva desta afirmação nos diz que
se uma função não é contínua num ponto, então ela não é diferenciável neste ponto.
Ou seja, quando queremos testar se uma função é diferenciável, podemos primeiro verificar se ela é contínua. Se for, então
talvez ela seja diferenciável, porém se não for então
com certeza não é diferenciável. Na primeira questão caso tivesse testado a continuidade veria que existia a possibilidade de ser diferenciável.
Na segunda questão temos

enquanto que

. Como os limites terais são distintos, então a função não é contínua neste ponto, e pelo teorema não é diferenciável.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jemourafer » Dom Abr 29, 2012 21:49
por jemourafer » Dom Abr 29, 2012 21:49
-
jemourafer
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Abr 01, 2012 20:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por MarceloFantini » Seg Abr 30, 2012 18:59
por MarceloFantini » Seg Abr 30, 2012 18:59
Você fez as contas da derivada pela definição de limite ao invés de calcular o limite da função. É aí o seu erro.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jemourafer » Qui Mai 03, 2012 20:34
por jemourafer » Qui Mai 03, 2012 20:34
Muuito obrigada. Agora sim entendi!

-
jemourafer
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Abr 01, 2012 20:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Continuidade
por AlbertoAM » Seg Abr 04, 2011 20:59
- 8 Respostas
- 5687 Exibições
- Última mensagem por LuizAquino

Qua Abr 06, 2011 10:33
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade
por guilherme5088 » Sáb Out 12, 2019 15:31
- 1 Respostas
- 5333 Exibições
- Última mensagem por adauto martins

Ter Out 15, 2019 23:11
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade
por MCordeiro » Qui Jul 16, 2020 19:11
- 1 Respostas
- 3540 Exibições
- Última mensagem por adauto martins

Qua Out 14, 2020 12:00
Cálculo: Limites, Derivadas e Integrais
-
- Exercicio de Continuidade
por PeIdInHu » Qua Jul 14, 2010 21:04
- 2 Respostas
- 3065 Exibições
- Última mensagem por PeIdInHu

Qui Jul 15, 2010 01:03
Cálculo: Limites, Derivadas e Integrais
-
- Limite Continuidade
por Claudin » Sáb Out 01, 2011 11:33
- 10 Respostas
- 5810 Exibições
- Última mensagem por Claudin

Seg Out 03, 2011 10:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , se x<1; e
, se x<1; e ![f(x)=\frac{1}{\sqrt[]{x}} f(x)=\frac{1}{\sqrt[]{x}}](/latexrender/pictures/7bf247bc7b411982b7b188fef14e9a7b.png) , se x
, se x 1; a)f é diferenciável em x=1? b)f é contínua em x=1?
1; a)f é diferenciável em x=1? b)f é contínua em x=1? , se x<1; e
, se x<1; e ![f(x)=\frac{1}{\sqrt[]{x}} f(x)=\frac{1}{\sqrt[]{x}}](/latexrender/pictures/7bf247bc7b411982b7b188fef14e9a7b.png) , se x
, se x 1; a)f é diferenciável em x=1? b)f é contínua em x=1?
1; a)f é diferenciável em x=1? b)f é contínua em x=1? ; f não é diferenciável em x=1 pois se fosse, f seria contínua em x=1.
; f não é diferenciável em x=1 pois se fosse, f seria contínua em x=1. existir.
existir.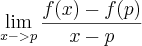 =
=  :.
:. ![\lim_{x->1+}\frac{\frac{1}{\sqrt[]{x}}-\frac{1}{\sqrt[]{1}}}{x-1}=-\frac{1}{2} \lim_{x->1+}\frac{\frac{1}{\sqrt[]{x}}-\frac{1}{\sqrt[]{1}}}{x-1}=-\frac{1}{2}](/latexrender/pictures/604fef5bfae41462756f094dd03883e6.png) . Como
. Como  , concluímos que o limite bilateral existe e então podemos dizer que f(x) é derivável em x=1. A função também é contínua em x=1, pois é derivável nesse ponto. Essa minha resposta está de acordo com o gabarito!
, concluímos que o limite bilateral existe e então podemos dizer que f(x) é derivável em x=1. A função também é contínua em x=1, pois é derivável nesse ponto. Essa minha resposta está de acordo com o gabarito! (que está de acordo com o gabarito), mas quando
(que está de acordo com o gabarito), mas quando  deveria valer -1/2 como na questão anterior, no gabarito diz que vale 1. No que eu errei?
deveria valer -1/2 como na questão anterior, no gabarito diz que vale 1. No que eu errei?

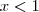 temos que
temos que  , enquanto que para
, enquanto que para 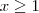 temos
temos  . Calculando os limites laterais, vemos
. Calculando os limites laterais, vemos  e
e  . Como coincidem, o limite existe e a função é diferenciável no ponto, portanto contínua.
. Como coincidem, o limite existe e a função é diferenciável no ponto, portanto contínua. na origem, ou de forma mais extrema procure sobre a
na origem, ou de forma mais extrema procure sobre a  enquanto que
enquanto que  . Como os limites terais são distintos, então a função não é contínua neste ponto, e pelo teorema não é diferenciável.
. Como os limites terais são distintos, então a função não é contínua neste ponto, e pelo teorema não é diferenciável.



![\lim_{x->1+}\frac{\frac{1}{\sqrt[]{x}}-\frac{1}{\sqrt[]{1}}}{x-1}= \lim_{x->1+}\frac{\frac{1-\sqrt[]{x}}{\sqrt[]{x}}}{x-1}= \lim_{x->1+}\frac{\frac{1}{\sqrt[]{x}}-\frac{1}{\sqrt[]{1}}}{x-1}= \lim_{x->1+}\frac{\frac{1-\sqrt[]{x}}{\sqrt[]{x}}}{x-1}=](/latexrender/pictures/c6d5665205758ff973439858642ff8a7.png)
![\lim_{x->1+}\frac{1-\sqrt[]{x}}{\sqrt[]{x}(x-1)}= \lim_{x->1+}\frac{1-\sqrt[]{x}}{\sqrt[]{x}(x-1)}=](/latexrender/pictures/eeb56b9df0011a388763f8286e646644.png)
![\lim_{x->1+}\frac{1-\sqrt[]{x}}{\sqrt[]{x}(x-1)}\frac{(1+\sqrt[]{x})}{(1+\sqrt[]{x})}= \lim_{x->1+}\frac{1-\sqrt[]{x}}{\sqrt[]{x}(x-1)}\frac{(1+\sqrt[]{x})}{(1+\sqrt[]{x})}=](/latexrender/pictures/e428fabad833dc0cd9a79867a10aa3c6.png)
![\lim_{x->1+}\frac{1+\sqrt[]{x}-\sqrt[]{x}-x}{\sqrt[]{x}(x-1)(1+\sqrt[]{x})}= \lim_{x->1+}\frac{1+\sqrt[]{x}-\sqrt[]{x}-x}{\sqrt[]{x}(x-1)(1+\sqrt[]{x})}=](/latexrender/pictures/16b4a597a31db09b383e55f593f501d3.png)
![\lim_{x->1+}\frac{1-x}{\sqrt[]{x}(x-1)(1+\sqrt[]{x})}= \lim_{x->1+}\frac{1-x}{\sqrt[]{x}(x-1)(1+\sqrt[]{x})}=](/latexrender/pictures/fd142ad9077de6c2975ee36103bee040.png)
![\lim_{x->1+}-\frac{1}{(\sqrt[]{x})(1+\sqrt[]{x})}= \lim_{x->1+}-\frac{1}{(\sqrt[]{x})(1+\sqrt[]{x})}=](/latexrender/pictures/461ee1846c683cde9462e58ab1e2a624.png)
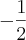 .
. e
e  . E como você pode ver nas minhas contas, meus limites laterais deram o mesmo resultado
. E como você pode ver nas minhas contas, meus limites laterais deram o mesmo resultado 






