Nas duas semanas seguintes à inauguração de mais uma loja de uma rede de supermercados, os produtos foram colocados à venda com preços 20% menores que os das demais lojas da rede. No final da promoção, o encarregado da loja determinou que o preço de cada mercadoria fosse aumentado em 20% para voltar aos preços anteriores, e por isso levou uma bronca do gerente. Explique o equívoco do encarregado, considerando uma mercadoria que na promoção custava R$ 80,00.
Eu resolvi pela regra de três simples, mas eu não estou compreendendo a parte que ele cita do equivoco. Alguém poderia me ajudar? Pela resolução eu obtive o resultado R$ 96,00, pois como o preço que ele deu já estava na promoção (R$80,00).


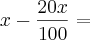
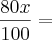
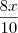
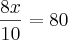
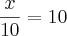
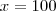
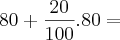
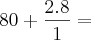
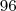




 , avisa que eu resolvo.
, avisa que eu resolvo.

