 por Cleyson007 » Ter Abr 24, 2012 09:50
por Cleyson007 » Ter Abr 24, 2012 09:50
Bom dia a todos!
Mostre que a função f: Z --> Z dada pela lei f(n)=2n é injetora mas não é sobrejetora.
Acredito que posso mostrar que ela é injetora da seguinte forma:
Sejam x1 e x2 pertencente a Z, com x1 e x2 diferente de 0.
f(x1)=f(x2), logo 2x1=2x2. Daí concluo que x1=x2 (Logo, f é injetiva).
Dúvida: Como mostrar que a função em questão não é sobrejetora?
Aguardo retorno.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Russman » Ter Abr 24, 2012 10:17
por Russman » Ter Abr 24, 2012 10:17
Para que a função f(x): A-> B seja sobrejetora é necessário que para todo y pertencente a B exista um x pertencente a A tal que y = f(x).
Veja que esta função se define para valores inteiros de n. Assim,
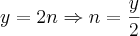
.
Portanto, só iremos obter valores de n para y múltiplo de 2 pois, do cont?ario, n não será inteiro. Assim, f(n) = 2n ? Z->Z não é sobrejetora.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Cleyson007 » Ter Abr 24, 2012 11:48
por Cleyson007 » Ter Abr 24, 2012 11:48
Bom dia Russman!
Nossa, muito simples.. Se y assumir valores ímpares contraria a condição da função está definida em Z.
Russman, obrigado pela ajuda.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Russman » Ter Abr 24, 2012 16:50
por Russman » Ter Abr 24, 2012 16:50
Exato!
Não por isso.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função sobrejetora
por leandrofontesantos » Seg Set 29, 2014 13:08
- 3 Respostas
- 1735 Exibições
- Última mensagem por adauto martins

Sáb Out 04, 2014 12:22
Funções
-
- Função injetora, sobrejetora.. par, ímpar?
por Jonatan » Sex Jul 30, 2010 11:59
- 1 Respostas
- 2082 Exibições
- Última mensagem por MarceloFantini

Sex Jul 30, 2010 15:08
Funções
-
- [Função Injetora, Sobrejetora] Dúvida exerícicios
por Eduardo_GNR » Qui Mar 14, 2013 21:41
- 1 Respostas
- 1403 Exibições
- Última mensagem por e8group

Sex Mar 15, 2013 12:15
Funções
-
- Transformações lineares injetoras e sobrejetora!
 por Manoella » Sáb Jan 22, 2011 14:16
por Manoella » Sáb Jan 22, 2011 14:16
- 4 Respostas
- 8681 Exibições
- Última mensagem por LuizAquino

Seg Jan 24, 2011 10:07
Álgebra Linear
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5588 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



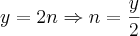 .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
