 por emsbp » Qui Abr 19, 2012 19:13
por emsbp » Qui Abr 19, 2012 19:13
Boa tarde.
O exercício é para calcular
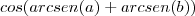
.
Comecei por aplicar regras das funções trigonométricas inversas:
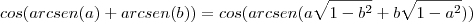
. A partir deste ponto não estou a conseguir chegar à solução dada:
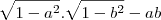
.
Qual o passo que devo seguir?
Obrigado!
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por DanielFerreira » Sáb Abr 21, 2012 18:25
por DanielFerreira » Sáb Abr 21, 2012 18:25
Outra forma:
emsbp escreveu:Boa tarde.
O exercício é para calcular
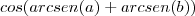
.
Comecei por aplicar regras das funções trigonométricas inversas:
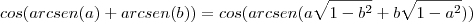
. A partir deste ponto não estou a conseguir chegar à solução dada:
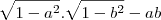
.
Qual o passo que devo seguir?
Obrigado!
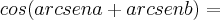
Consideremos:
I)
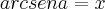
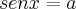
============de== sen²x + cos²x = 1======temos==========>
![cos x = \sqrt[]{1 - sen^2 x} cos x = \sqrt[]{1 - sen^2 x}](/latexrender/pictures/bb9ea8573fcc9933bf140e523d4be304.png)
==========>
![cos x = \sqrt[]{1 - a^2} cos x = \sqrt[]{1 - a^2}](/latexrender/pictures/bb73dfbd599fafb3f641546a641a9bdb.png)
II)
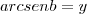
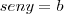
============de== sen²x + cos²x = 1======temos==========>
![cos y = \sqrt[]{1 - sen^2 y} cos y = \sqrt[]{1 - sen^2 y}](/latexrender/pictures/fac7fc4d625154a7caa3602c9724ed7a.png)
==========>
![cos y = \sqrt[]{1 - b^2} cos y = \sqrt[]{1 - b^2}](/latexrender/pictures/1d889d1cfd1fb823eb3e5e4b65e837db.png)
continuando...
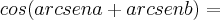

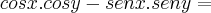
![(\sqrt[]{1 - a^2})(\sqrt[]{1 - b^2}) - ab (\sqrt[]{1 - a^2})(\sqrt[]{1 - b^2}) - ab](/latexrender/pictures/7a1f51b428a2654a857e09516f8ad839.png)
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por emsbp » Dom Abr 22, 2012 17:43
por emsbp » Dom Abr 22, 2012 17:43
Muito obrigado!
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por DanielFerreira » Ter Abr 24, 2012 20:14
por DanielFerreira » Ter Abr 24, 2012 20:14
vlw.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- trigonometria-funçoes inversas
por henrique_mat » Seg Ago 23, 2010 18:57
- 4 Respostas
- 2621 Exibições
- Última mensagem por henrique_mat

Ter Ago 24, 2010 20:59
Trigonometria
-
- [calculo] funções inversas
por beel » Dom Out 16, 2011 00:53
- 1 Respostas
- 1266 Exibições
- Última mensagem por LuizAquino

Seg Out 17, 2011 12:43
Cálculo: Limites, Derivadas e Integrais
-
- [funções inversas]
por Ana_Rodrigues » Ter Jan 24, 2012 17:46
- 2 Respostas
- 1742 Exibições
- Última mensagem por Ana_Rodrigues

Ter Jan 24, 2012 22:33
Funções
-
- funções inversas
por Edgard Guarido » Sex Mar 07, 2014 18:53
- 2 Respostas
- 2616 Exibições
- Última mensagem por Edgard Guarido

Qui Mar 13, 2014 15:54
Funções
-
- Funções circulares inversas
por Ananda » Qui Mar 20, 2008 20:03
- 2 Respostas
- 4810 Exibições
- Última mensagem por Ananda

Seg Mar 24, 2008 17:13
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
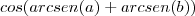 .
.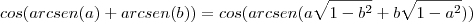 . A partir deste ponto não estou a conseguir chegar à solução dada:
. A partir deste ponto não estou a conseguir chegar à solução dada: 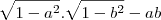 .
.
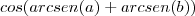 .
.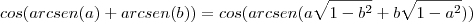 . A partir deste ponto não estou a conseguir chegar à solução dada:
. A partir deste ponto não estou a conseguir chegar à solução dada: 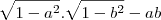 .
.
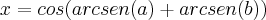
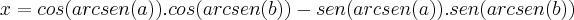
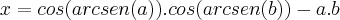
![senx=\sqrt[]{1 - cos^2 x} senx=\sqrt[]{1 - cos^2 x}](/latexrender/pictures/518f7ae4cdfdb43b5488ef22403eba1a.png)
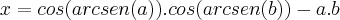
![x=\sqrt[]{1 - sen^2 (arcsen(a))}.\sqrt[]{1 - sen^2 (arcsen(b))} - a.b x=\sqrt[]{1 - sen^2 (arcsen(a))}.\sqrt[]{1 - sen^2 (arcsen(b))} - a.b](/latexrender/pictures/be545bd2756e1e14201edd61d71a97e3.png)
![x=\sqrt[]{1 - a^2}\sqrt[]{1 -b^2}- a.b x=\sqrt[]{1 - a^2}\sqrt[]{1 -b^2}- a.b](/latexrender/pictures/c123257ea85a11bceaf613bcad8d0201.png)

.
. A partir deste ponto não estou a conseguir chegar à solução dada:
.
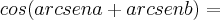
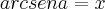
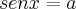 ============de== sen²x + cos²x = 1======temos==========>
============de== sen²x + cos²x = 1======temos==========> ![cos x = \sqrt[]{1 - sen^2 x} cos x = \sqrt[]{1 - sen^2 x}](/latexrender/pictures/bb9ea8573fcc9933bf140e523d4be304.png) ==========>
==========> ![cos x = \sqrt[]{1 - a^2} cos x = \sqrt[]{1 - a^2}](/latexrender/pictures/bb73dfbd599fafb3f641546a641a9bdb.png)
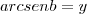
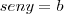 ============de== sen²x + cos²x = 1======temos==========>
============de== sen²x + cos²x = 1======temos==========> ![cos y = \sqrt[]{1 - sen^2 y} cos y = \sqrt[]{1 - sen^2 y}](/latexrender/pictures/fac7fc4d625154a7caa3602c9724ed7a.png) ==========>
==========> ![cos y = \sqrt[]{1 - b^2} cos y = \sqrt[]{1 - b^2}](/latexrender/pictures/1d889d1cfd1fb823eb3e5e4b65e837db.png)
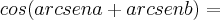

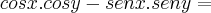
![(\sqrt[]{1 - a^2})(\sqrt[]{1 - b^2}) - ab (\sqrt[]{1 - a^2})(\sqrt[]{1 - b^2}) - ab](/latexrender/pictures/7a1f51b428a2654a857e09516f8ad839.png)





 , avisa que eu resolvo.
, avisa que eu resolvo.

