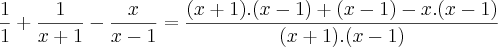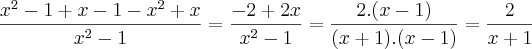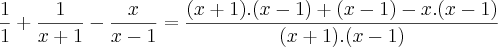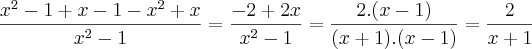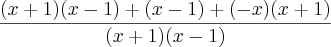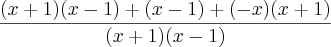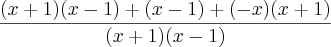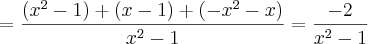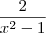por LuizCarlos » Sex Abr 20, 2012 13:09
por LuizCarlos » Sex Abr 20, 2012 13:09
Olá amigos,
estou resolvendo umas contas de frações algébricas, mas essa aqui, não está dando resultado correto!
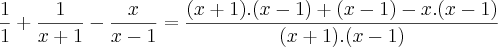
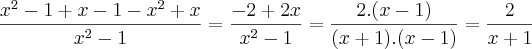
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Cleyson007 » Sex Abr 20, 2012 14:04
por Cleyson007 » Sex Abr 20, 2012 14:04
Boa tarde Luiz Carlos!
Luiz, parabéns o m.m.c está correto!
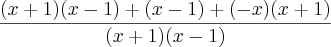
Repare que você cometeu um pequeno erro na primeira parte. Tente refazer pelo que deixei escrito.
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por LuizCarlos » Sex Abr 20, 2012 14:48
por LuizCarlos » Sex Abr 20, 2012 14:48
Cleyson007 escreveu:Boa tarde Luiz Carlos!
Luiz, parabéns o m.m.c está correto!
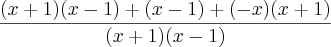
Repare que você cometeu um pequeno erro na primeira parte. Tente refazer pelo que deixei escrito.
Comente qualquer dúvida

Até mais.
Olá amigo Cleyson007 obrigado pelo elogio e pela ajuda, estou me esforçando para aprender matemática, e frações algébricas =D.
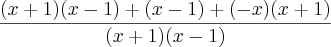
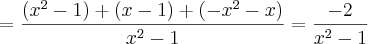
O resultado no livro é
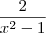
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Cleyson007 » Sex Abr 20, 2012 15:07
por Cleyson007 » Sex Abr 20, 2012 15:07
Boa tarde amigo Luiz!
Luiz, com certeza o seu esforço será recompensado..
Quanto a resposta, não encontrei erro algum, ok?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por LuizCarlos » Sex Abr 20, 2012 17:13
por LuizCarlos » Sex Abr 20, 2012 17:13
Cleyson007 escreveu:Boa tarde amigo Luiz!
Luiz, com certeza o seu esforço será recompensado..
Quanto a resposta, não encontrei erro algum, ok?
Até mais.
Certo, muito obrigado amigo cleyson007, por me ajudar! Deus te ajude também! abraço e tudo de bom para você e sua família!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Cleyson007 » Sex Abr 20, 2012 17:44
por Cleyson007 » Sex Abr 20, 2012 17:44
Boa tarde amigo Luiz!
Para mim é um prazer ajudar.. Sempre que o puder, fique certo de que o farei.
Com certeza Deus nos ajuda e nos torna pessoas ainda melhores..
Também estendo os cumprimentos à você e sua família. Bom final de semana!
Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Fração Algébrica
por Lucio » Qua Dez 21, 2011 07:48
- 3 Respostas
- 2193 Exibições
- Última mensagem por fraol

Qua Dez 21, 2011 22:31
Polinômios
-
- Re: Fração algébrica
por LuizCarlos » Sáb Abr 21, 2012 09:10
- 5 Respostas
- 2618 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 21, 2012 16:44
Álgebra Elementar
-
- Fração algébrica
por LuizCarlos » Sáb Abr 21, 2012 19:04
- 6 Respostas
- 2906 Exibições
- Última mensagem por Russman

Sáb Abr 21, 2012 20:40
Álgebra Elementar
-
- Divisão de fração algébrica
por lucas7 » Seg Fev 21, 2011 18:09
- 3 Respostas
- 2423 Exibições
- Última mensagem por lucas7

Seg Fev 21, 2011 22:16
Álgebra Elementar
-
- Divisão de fração algébrica 2
por lucas7 » Seg Fev 21, 2011 21:37
- 10 Respostas
- 5394 Exibições
- Última mensagem por lucas7

Ter Fev 22, 2011 17:26
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.