Num prédio existem 2 elevadores. O elevador A é utilizado por 40% dos moradores e avaria com uma probabilidade de 2%. O elevador B é utilizado por 60% dos moradores e tem uma probabilidade de avariar de 3%
Sejam agora os seguintes acontecimentos:
X-"Utilizar o elevador A."
Y-"O elevador está avariado"
Do enunciado eu deduzi que o elevador avaria quando é utilizado.Até podia estar avariado antes de ser utilizado, mas a avaria so é detetada quando o elevador é utilizado.Está á a parte intuitiva do problema.
Logo, a probabilidade de o elevador avariar só se verifica quando o mesmo é utilizado.Assim:
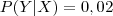e 
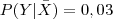
Recorrendo à definição de probabilidade condicionada, chegamos a
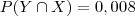e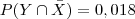 
Qual é a diferença na interpretação entre as probabilidades condicionadas, anteriormente calculadas, e as probabilidades da interceção?
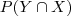ou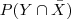 
no contexto do enunciado?!?
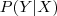dá-nos a probabilidade de estar avariado dado ter sido utilizado, neste caso o elevador 
Utilizar o elevador A e ele sofrer avaria 
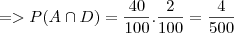
Utilizar o elevador B e ele sofrer avaria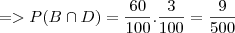 
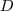- O elevador estar avariado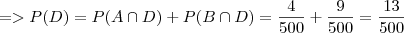 
.
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.