 por Henrique Bueno » Dom Abr 15, 2012 14:31
por Henrique Bueno » Dom Abr 15, 2012 14:31
O limite dado é o seguinte:
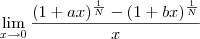
sei que o resultado é
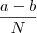
por recorrência, afinal fiz com N=2,N=3 e N=4 e foi isso que obtive, mas não consigo partir do limite dado e chegar nessa resposta
grato pela atenção
-
Henrique Bueno
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Mar 02, 2011 19:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Seg Abr 16, 2012 16:09
por LuizAquino » Seg Abr 16, 2012 16:09
Henrique Bueno escreveu:O limite dado é o seguinte:
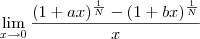
sei que o resultado é
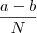
por recorrência, afinal fiz com N=2,N=3 e N=4 e foi isso que obtive, mas não consigo partir do limite dado e chegar nessa resposta
Esse limite é equivalente a:
![\lim_{x\to 0} \dfrac{\sqrt[N]{1+ax} - \sqrt[N]{1+bx}}{x} \lim_{x\to 0} \dfrac{\sqrt[N]{1+ax} - \sqrt[N]{1+bx}}{x}](/latexrender/pictures/8089df1001a4db6fdb55a36f3eceedfc.png)
Para resolvê-lo, você precisa usar o seguinte produto notável:
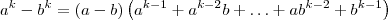
Note que no segundo fator temos uma soma que tem k parcelas. Para perceber melhor isso, observe por exemplo esse produto notável para k = 5:
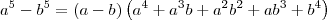
Vamos então multiplicar o numerador e o denominador da fração no limite por:
![\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right) \left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)](/latexrender/pictures/e1fb8084d601df16524cb16ab1ad2637.png)
Note que essa expressão tem N parcelas. Além disso, ao multiplicar essa expressão pelo numerador, teremos o produto notável indicado anteriormente para k = N:
![\left(\sqrt[N]{1 + ax} - \sqrt[N]{1 + bx}\right)\, \left(\sqrt[N]{1 + ax} - \sqrt[N]{1 + bx}\right)\,](/latexrender/pictures/552e312ff2e0a5ae908d9841c979179b.png)
![\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)= \left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)=](/latexrender/pictures/390ddf08c41a798da80585ad12e505ab.png)
![= \left(\sqrt[N]{1 + ax}\right)^N - \left(\sqrt[N]{1 + bx}\right)^N = (1 + ax) - (1 + bx) = (a-b)x = \left(\sqrt[N]{1 + ax}\right)^N - \left(\sqrt[N]{1 + bx}\right)^N = (1 + ax) - (1 + bx) = (a-b)x](/latexrender/pictures/60a50dee1b548f77b28609509c67ea05.png)
Agora note que quando
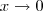
, temos que
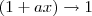
e
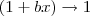
.
Sendo assim, quando
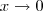
temos que aquela expressão que nós multiplicamos será igual a:
![\left(\sqrt[N]{1}^{N-1} + \sqrt[N]{1}^{N-2}\sqrt[N]{1} + \ldots + \sqrt[N]{1}\sqrt[N]{1}^{N-2} + \sqrt[N]{1}^{N-1}\right) = \left(\sqrt[N]{1}^{N-1} + \sqrt[N]{1}^{N-2}\sqrt[N]{1} + \ldots + \sqrt[N]{1}\sqrt[N]{1}^{N-2} + \sqrt[N]{1}^{N-1}\right) =](/latexrender/pictures/cf648cff8cb7516734f2a3fe1aa6ce8c.png)
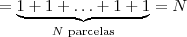
Usando todas essas informações, temos que:
![\lim_{x\to 0} \dfrac{\sqrt[N]{1+ax} - \sqrt[N]{1+bx}}{x} = \lim_{x\to 0} \dfrac{\sqrt[N]{1+ax} - \sqrt[N]{1+bx}}{x} =](/latexrender/pictures/90075713736f7cabb3c62894c994134e.png)
![= \lim_{x\to 0} \dfrac{\left(\sqrt[N]{1 + ax}\right)^N - \left(\sqrt[N]{1 + bx}\right)^N}{x\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)} = \lim_{x\to 0} \dfrac{\left(\sqrt[N]{1 + ax}\right)^N - \left(\sqrt[N]{1 + bx}\right)^N}{x\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)}](/latexrender/pictures/d88f2338bc3931bc9c0f9c0da8e048c7.png)
![= \lim_{x\to 0} \dfrac{(a-b)x}{x\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)} = \lim_{x\to 0} \dfrac{(a-b)x}{x\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)}](/latexrender/pictures/d15ea6e2a45881140c5a5064c0b75e9f.png)
![= \lim_{x\to 0} \dfrac{a-b}{\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}} = \lim_{x\to 0} \dfrac{a-b}{\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}}](/latexrender/pictures/ca119c2256a946aa5d175afdcccd55a5.png)
![= \dfrac{a-b}{\sqrt[N]{1}^{N-1} + \sqrt[N]{1}^{N-2}\sqrt[N]{1} + \ldots + \sqrt[N]{1}\sqrt[N]{1}^{N-2} + \sqrt[N]{1}^{N-1}} = \dfrac{a-b}{\sqrt[N]{1}^{N-1} + \sqrt[N]{1}^{N-2}\sqrt[N]{1} + \ldots + \sqrt[N]{1}\sqrt[N]{1}^{N-2} + \sqrt[N]{1}^{N-1}}](/latexrender/pictures/a7b0d2dc63b5d2d3250b45b5506c3d93.png)
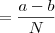
Editado pela última vez por
LuizAquino em Seg Abr 16, 2012 20:00, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Henrique Bueno » Seg Abr 16, 2012 19:08
por Henrique Bueno » Seg Abr 16, 2012 19:08
Muito bom luiz! muito obrigado ! Com um exercício o senhor foi capaz de esclarecer muitas dúvidas minhas !
-
Henrique Bueno
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Mar 02, 2011 19:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4808 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limites infinitos envolvendo série
 por davifd_ » Ter Ago 18, 2015 15:56
por davifd_ » Ter Ago 18, 2015 15:56
- 10 Respostas
- 10649 Exibições
- Última mensagem por nakagumahissao

Qua Ago 19, 2015 09:17
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo I] Limites envolvendo raízes.
por Jefferson_mcz » Seg Mar 18, 2013 14:00
- 1 Respostas
- 1717 Exibições
- Última mensagem por young_jedi

Seg Mar 18, 2013 20:35
Cálculo: Limites, Derivadas e Integrais
-
- Limite( Cálculo de limites sem a utilização L'hôspital )
 por brunotorres123-abc » Dom Abr 05, 2015 14:55
por brunotorres123-abc » Dom Abr 05, 2015 14:55
- 0 Respostas
- 1153 Exibições
- Última mensagem por brunotorres123-abc

Dom Abr 05, 2015 14:55
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Calculo de limite usando o teorema do confronto.
por erickm93 » Qua Mai 22, 2013 10:48
- 3 Respostas
- 6019 Exibições
- Última mensagem por erickm93

Qua Mai 22, 2013 23:49
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
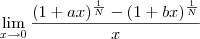
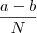 por recorrência, afinal fiz com N=2,N=3 e N=4 e foi isso que obtive, mas não consigo partir do limite dado e chegar nessa resposta
por recorrência, afinal fiz com N=2,N=3 e N=4 e foi isso que obtive, mas não consigo partir do limite dado e chegar nessa resposta
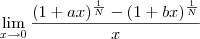
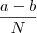 por recorrência, afinal fiz com N=2,N=3 e N=4 e foi isso que obtive, mas não consigo partir do limite dado e chegar nessa resposta
por recorrência, afinal fiz com N=2,N=3 e N=4 e foi isso que obtive, mas não consigo partir do limite dado e chegar nessa resposta
por recorrência, afinal fiz com N=2,N=3 e N=4 e foi isso que obtive, mas não consigo partir do limite dado e chegar nessa resposta
![\lim_{x\to 0} \dfrac{\sqrt[N]{1+ax} - \sqrt[N]{1+bx}}{x} \lim_{x\to 0} \dfrac{\sqrt[N]{1+ax} - \sqrt[N]{1+bx}}{x}](/latexrender/pictures/8089df1001a4db6fdb55a36f3eceedfc.png)
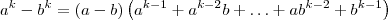
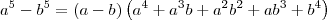
![\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right) \left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)](/latexrender/pictures/e1fb8084d601df16524cb16ab1ad2637.png)
![\left(\sqrt[N]{1 + ax} - \sqrt[N]{1 + bx}\right)\, \left(\sqrt[N]{1 + ax} - \sqrt[N]{1 + bx}\right)\,](/latexrender/pictures/552e312ff2e0a5ae908d9841c979179b.png)
![\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)= \left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)=](/latexrender/pictures/390ddf08c41a798da80585ad12e505ab.png)
![= \left(\sqrt[N]{1 + ax}\right)^N - \left(\sqrt[N]{1 + bx}\right)^N = (1 + ax) - (1 + bx) = (a-b)x = \left(\sqrt[N]{1 + ax}\right)^N - \left(\sqrt[N]{1 + bx}\right)^N = (1 + ax) - (1 + bx) = (a-b)x](/latexrender/pictures/60a50dee1b548f77b28609509c67ea05.png)
 , temos que
, temos que  e
e 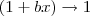 .
.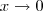 temos que aquela expressão que nós multiplicamos será igual a:
temos que aquela expressão que nós multiplicamos será igual a:![\left(\sqrt[N]{1}^{N-1} + \sqrt[N]{1}^{N-2}\sqrt[N]{1} + \ldots + \sqrt[N]{1}\sqrt[N]{1}^{N-2} + \sqrt[N]{1}^{N-1}\right) = \left(\sqrt[N]{1}^{N-1} + \sqrt[N]{1}^{N-2}\sqrt[N]{1} + \ldots + \sqrt[N]{1}\sqrt[N]{1}^{N-2} + \sqrt[N]{1}^{N-1}\right) =](/latexrender/pictures/cf648cff8cb7516734f2a3fe1aa6ce8c.png)
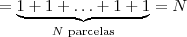
![\lim_{x\to 0} \dfrac{\sqrt[N]{1+ax} - \sqrt[N]{1+bx}}{x} = \lim_{x\to 0} \dfrac{\sqrt[N]{1+ax} - \sqrt[N]{1+bx}}{x} =](/latexrender/pictures/90075713736f7cabb3c62894c994134e.png)
![= \lim_{x\to 0} \dfrac{\left(\sqrt[N]{1 + ax}\right)^N - \left(\sqrt[N]{1 + bx}\right)^N}{x\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)} = \lim_{x\to 0} \dfrac{\left(\sqrt[N]{1 + ax}\right)^N - \left(\sqrt[N]{1 + bx}\right)^N}{x\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)}](/latexrender/pictures/d88f2338bc3931bc9c0f9c0da8e048c7.png)
![= \lim_{x\to 0} \dfrac{(a-b)x}{x\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)} = \lim_{x\to 0} \dfrac{(a-b)x}{x\left(\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}\right)}](/latexrender/pictures/d15ea6e2a45881140c5a5064c0b75e9f.png)
![= \lim_{x\to 0} \dfrac{a-b}{\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}} = \lim_{x\to 0} \dfrac{a-b}{\sqrt[N]{1 + ax}^{N-1} + \sqrt[N]{1 + ax}^{N-2}\sqrt[N]{1 + bx} + \ldots + \sqrt[N]{1 + ax}\sqrt[N]{1 + bx}^{N-2} + \sqrt[N]{1 + bx}^{N-1}}](/latexrender/pictures/ca119c2256a946aa5d175afdcccd55a5.png)
![= \dfrac{a-b}{\sqrt[N]{1}^{N-1} + \sqrt[N]{1}^{N-2}\sqrt[N]{1} + \ldots + \sqrt[N]{1}\sqrt[N]{1}^{N-2} + \sqrt[N]{1}^{N-1}} = \dfrac{a-b}{\sqrt[N]{1}^{N-1} + \sqrt[N]{1}^{N-2}\sqrt[N]{1} + \ldots + \sqrt[N]{1}\sqrt[N]{1}^{N-2} + \sqrt[N]{1}^{N-1}}](/latexrender/pictures/a7b0d2dc63b5d2d3250b45b5506c3d93.png)
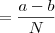


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
