 por Anderson Alves » Dom Abr 08, 2012 21:10
por Anderson Alves » Dom Abr 08, 2012 21:10
Olá Galera.
Estou com dúvidas nestes dois exercícios.
1) O termo geral de uma Progressão Aritmética é an= 0,3 - 0,05n. Qual a razão desta progressão?
Resp.: -0,05
2) O termo geral de uma Progressão Aritmética com um número ímpar de termos é 2n + 1. Qual o termo médio desta progressão?
Res.: n + 2.
Em nenhum destes eu consegui desenvolver as questões
Ficarei grato pela ajuda..
-
Anderson Alves
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Sex Fev 24, 2012 22:39
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Informática
- Andamento: formado
 por MarceloFantini » Seg Abr 09, 2012 03:44
por MarceloFantini » Seg Abr 09, 2012 03:44
No primeiro item, perceba que o termo geral é da forma
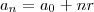
, onde

é a razão. Daí conclua a resposta.
No segundo, acho estranho. Esse

que aparece na resposta seria o número de termos da progressão?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Anderson Alves » Qui Abr 12, 2012 22:41
por Anderson Alves » Qui Abr 12, 2012 22:41
Certo. Mas como devo concretizar a questão 1?
E a questão 2, pois é, eu tenho como resposta n + 2, podendo ser o número de termos.
O problema é que eu não consegui desenvolver essas questões.
Valeu pela ajuda....
-
Anderson Alves
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Sex Fev 24, 2012 22:39
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Informática
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Progressões aritméticas
por Alessandrasouza » Sex Mai 14, 2010 15:44
- 3 Respostas
- 2085 Exibições
- Última mensagem por Cleyson007

Sáb Mai 15, 2010 10:41
Progressões
-
- Progressões Aritméticas
por Anderson Alves » Sáb Abr 07, 2012 01:13
- 2 Respostas
- 1319 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 07, 2012 01:31
Progressões
-
- Progressões Aritméticas
por Anderson Alves » Sáb Abr 14, 2012 13:42
- 1 Respostas
- 1671 Exibições
- Última mensagem por Lucio Carvalho

Sáb Abr 14, 2012 16:46
Progressões
-
- Progressões Aritméticas
por MarinaM » Dom Abr 15, 2012 00:24
- 2 Respostas
- 1834 Exibições
- Última mensagem por DanielFerreira

Dom Abr 15, 2012 19:56
Progressões
-
- Progressões Aritméticas
por Anderson Alves » Ter Abr 17, 2012 22:30
- 3 Respostas
- 2009 Exibições
- Última mensagem por Russman

Qui Jun 21, 2012 21:46
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


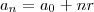 , onde
, onde  é a razão. Daí conclua a resposta.
é a razão. Daí conclua a resposta. que aparece na resposta seria o número de termos da progressão?
que aparece na resposta seria o número de termos da progressão?
