 por amanda costa » Ter Abr 10, 2012 21:39
por amanda costa » Ter Abr 10, 2012 21:39
Olá,
Tenho dúvidas no seguinte exercício.
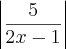

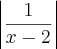
a primeira etapa da resolução seria:
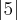
.


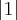
.
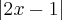
5x-10

2x -1
5x-10-2x+1

0
3x-9

0
x = 3
[3,

)
Porém, não sei como resolver a segunda .. sei que a resolução do exercício é (-

,
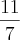
]

[3, +

) - {

}
alguém pode me explicar como resolvo isso passo a passo? obrigada
Editado pela última vez por
amanda costa em Ter Abr 10, 2012 22:52, em um total de 2 vezes.
-
amanda costa
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Abr 10, 2012 21:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Ter Abr 10, 2012 22:18
por MarceloFantini » Ter Abr 10, 2012 22:18
Amanda, sua inequação não está clara. Por favor, use LaTeX para redigir a fórmula. Para escrever uma fração em módulo use
- Código: Selecionar todos
\left| \frac{123}{456} \right|
que gera

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por amanda costa » Ter Abr 10, 2012 22:50
por amanda costa » Ter Abr 10, 2012 22:50
Já modifiquei
MarceloFantini escreveu:Amanda, sua inequação não está clara. Por favor, use LaTeX para redigir a fórmula. Para escrever uma fração em módulo use
- Código: Selecionar todos
\left| \frac{123}{456} \right|
que gera

.
-
amanda costa
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Abr 10, 2012 21:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INEQUAÇÂO] Inequação do tipo: (a+ x < b + x < c + x)
por Diofanto » Dom Fev 03, 2013 19:55
- 7 Respostas
- 6329 Exibições
- Última mensagem por Diofanto

Qui Fev 14, 2013 23:45
Inequações
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7401 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- Inequação
por Luna » Seg Set 28, 2009 18:55
- 4 Respostas
- 3743 Exibições
- Última mensagem por Molina

Ter Set 29, 2009 16:50
Sistemas de Equações
-
- Inequação
por Luna » Ter Set 29, 2009 16:48
- 1 Respostas
- 2121 Exibições
- Última mensagem por Molina

Qua Set 30, 2009 00:39
Sistemas de Equações
-
- Inequação
por Bebel » Dom Ago 08, 2010 00:50
- 0 Respostas
- 1628 Exibições
- Última mensagem por Bebel

Dom Ago 08, 2010 00:50
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
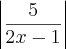


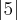 .
.

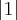 .
.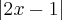
 2x -1
2x -1 0
0 0
0 )
) ,
, 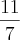 ]
]  [3, +
[3, + ) - {
) - { }
}

 .
.
