olá galera! preciso de ajuda pruma prova que terei nessa terça feira!! se puderem responder até lá, agradeceria muito!!
Dados os pontos: F = (1, -1, 1) , Q = (2, 0, 2), P= (2, 1, 4) e T = (3, 2, 5)
a) mostre que os pontos F, Q, P e T pertencem a um único plano, determinando suas equações paramétricas.
b) obtenha uma equação cartesiana para o plano do item anterior.
c) mostre que esses pontos são vértices de um paralelogramo.
d) calcule a área do paralelogramo
e) quais são os tamanhos das duas diagonais do paralelogramo?
só consegui provar a coplanaridade do item a, o resto não consegui nada ... Muito obrigada galera! são 1:50 da manhã e o desespero tomou conta de mim, como toma a todos os estudantes de engenharia!! boa noite!


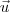 e
e  (partindo de uma mesma origem) representam lados consecutivos do paralelogramo, temos que:
(partindo de uma mesma origem) representam lados consecutivos do paralelogramo, temos que: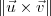 ;
; e
e  .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

