 por nietzsche » Dom Abr 08, 2012 18:57
por nietzsche » Dom Abr 08, 2012 18:57
Não está correto.
"Considerando tgx = u, teremos dx = du.cos²x" : Se u=sex/cos x, então du/dx ? cos²x.
Outra coisa, se você mudou a variável de integração, você precisa trocar todas as variáveis x por alguma função de um, ou seja, x "some" do integrando.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Guill » Dom Abr 08, 2012 19:00
por Guill » Dom Abr 08, 2012 19:00
nietzsche escreveu:Considerando tgx = u, teremos dx = du.cos²x" : Se u=sex/cos x, então du/dx ? cos²x.
Não é mesmo. É por isso que eu acredito que esteja ceto:
Se u=sex/cos x, então du/dx = 1/cos²x
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Dom Abr 08, 2012 19:04
por fraol » Dom Abr 08, 2012 19:04
No meu entendimento a solução de
Guill está correta. O que poderia ser complementado é a resposta em termos de
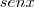
e

pela diferença dos logaritmos.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por nietzsche » Dom Abr 08, 2012 19:08
por nietzsche » Dom Abr 08, 2012 19:08
Desculpe, está certo essa passagem:
" "Considerando tgx = u, teremos dx = du.cos²x" : Se u=sen x/cos x, então du/dx ? cos²x. "
É isso mesmo, du/dx = 1/ cos²x.
Mas quando vc muda a variável vc não pode fazer isso:

Não pode aparecer o x, pois contaria o teorema da mudança de variáveis.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por nietzsche » Dom Abr 08, 2012 19:20
por nietzsche » Dom Abr 08, 2012 19:20
Enunciado do teorema a que me refiro:
Let I

be an interval and g : [a,b]

I be a continuously differentiable function. Suppose that f : I

is a continuous function. Then

fonte:
http://en.wikipedia.org/wiki/Integratio ... bstitution
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Está, ou não está certo. Eis a questão!
por Thiago 86 » Dom Set 29, 2013 21:48
- 0 Respostas
- 2828 Exibições
- Última mensagem por Thiago 86

Dom Set 29, 2013 21:48
Funções
-
- CONFERIR SE ESTÁ CERTO
por gabimucedola » Sex Abr 02, 2010 18:11
- 1 Respostas
- 1561 Exibições
- Última mensagem por davi_11

Sáb Abr 03, 2010 13:37
Matemática Financeira
-
- Expressão Está certo ?
por LuizCarlos » Qui Ago 11, 2011 12:41
- 2 Respostas
- 1998 Exibições
- Última mensagem por LuizCarlos

Qui Ago 11, 2011 14:43
Álgebra Elementar
-
- Limites - Está certo?
por iceman » Dom Set 16, 2012 14:57
- 1 Respostas
- 1481 Exibições
- Última mensagem por young_jedi

Dom Set 16, 2012 16:17
Cálculo: Limites, Derivadas e Integrais
-
- simplifiquei e achei...está certo?????????????
por zig » Sex Set 23, 2011 13:57
- 3 Respostas
- 62993 Exibições
- Última mensagem por fraol

Dom Dez 11, 2011 20:24
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.












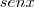 e
e  pela diferença dos logaritmos.
pela diferença dos logaritmos.


 be an interval and g : [a,b]
be an interval and g : [a,b]  I be a continuously differentiable function. Suppose that f : I
I be a continuously differentiable function. Suppose that f : I is a continuous function. Then
is a continuous function. Then



 , avisa que eu resolvo.
, avisa que eu resolvo.

