Grasi escreveu:Queremos construir uma lata cilíndrica, de volume 900 ml para servir de embalagem para óleo. Quais devem ser as medidas do raio da base e da altura para que a lata seja a mais econômica possível?
Já tentei encontrar a solução em 3 livros q tenho, mas os exemplos e teorias não estão me ajudando.
Peço a gentileza para ajudar-me, agradeço dede já. Muito obrigada!
Bom dia, Grasi.
Precisamos minimizar a área superficial da lata, que é dada por:
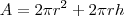
O volume é dado por
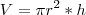
. Ou seja, nesse cado
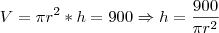
Ou seja, substituindo na equação da área, temos:
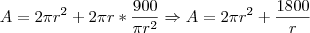
Devemos encontrar o mínimo desta função, logo, derivando A:
![A'=4 \pi r - \frac{1800}{r^2}=0 \Rightarrow r^3= \frac{1800}{4 \pi} \Rightarrow r=\sqrt[3]{\frac{450}{\pi}} A'=4 \pi r - \frac{1800}{r^2}=0 \Rightarrow r^3= \frac{1800}{4 \pi} \Rightarrow r=\sqrt[3]{\frac{450}{\pi}}](/latexrender/pictures/a8fd927ea03c128e1adfeb175ec60ed3.png)
Fazendo o teste da segunda derivada, temos que
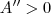
,
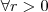
. Com isso
![r=\sqrt[3]{\frac{450}{\pi}} r=\sqrt[3]{\frac{450}{\pi}}](/latexrender/pictures/89927c8df6e07acc4435d8e00f189640.png)
é um ponto de mínimo local. Mas o gráfico de A é côncavo para cima e o ponto de mínimo local deve ser também o mínimo absoluto.
Conclusão: O raio ideal da base da lata é
![r=\sqrt[3]{\frac{450}{\pi}} r=\sqrt[3]{\frac{450}{\pi}}](/latexrender/pictures/89927c8df6e07acc4435d8e00f189640.png)
e a altura ideal dessa lata é
![h={\frac{900}{\pi * (\sqrt[3]{\frac{450}{\pi}})^2}=2*\sqrt[3]{\frac{450}{\pi}}=2r h={\frac{900}{\pi * (\sqrt[3]{\frac{450}{\pi}})^2}=2*\sqrt[3]{\frac{450}{\pi}}=2r](/latexrender/pictures/5a6031de7c35462e59c3694417eefa22.png)
Problema grande, porém, se analisar passo a passo verá que não terá grnades problemas.
Bom estudo,



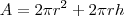
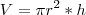 . Ou seja, nesse cado
. Ou seja, nesse cado 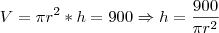
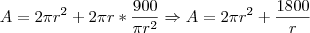
![A'=4 \pi r - \frac{1800}{r^2}=0 \Rightarrow r^3= \frac{1800}{4 \pi} \Rightarrow r=\sqrt[3]{\frac{450}{\pi}} A'=4 \pi r - \frac{1800}{r^2}=0 \Rightarrow r^3= \frac{1800}{4 \pi} \Rightarrow r=\sqrt[3]{\frac{450}{\pi}}](/latexrender/pictures/a8fd927ea03c128e1adfeb175ec60ed3.png)
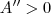 ,
, 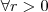 . Com isso
. Com isso ![r=\sqrt[3]{\frac{450}{\pi}} r=\sqrt[3]{\frac{450}{\pi}}](/latexrender/pictures/89927c8df6e07acc4435d8e00f189640.png) é um ponto de mínimo local. Mas o gráfico de A é côncavo para cima e o ponto de mínimo local deve ser também o mínimo absoluto.
é um ponto de mínimo local. Mas o gráfico de A é côncavo para cima e o ponto de mínimo local deve ser também o mínimo absoluto.![h={\frac{900}{\pi * (\sqrt[3]{\frac{450}{\pi}})^2}=2*\sqrt[3]{\frac{450}{\pi}}=2r h={\frac{900}{\pi * (\sqrt[3]{\frac{450}{\pi}})^2}=2*\sqrt[3]{\frac{450}{\pi}}=2r](/latexrender/pictures/5a6031de7c35462e59c3694417eefa22.png)


