 por Priscilla Correa » Sáb Abr 07, 2012 15:44
por Priscilla Correa » Sáb Abr 07, 2012 15:44
![\lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p \lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p](/latexrender/pictures/a7f22620032ff7aceba3a45471e3768d.png)
Alguém pode me ajudar??
-
Priscilla Correa
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Abr 07, 2012 08:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA
- Andamento: cursando
 por LuizAquino » Sáb Abr 07, 2012 16:06
por LuizAquino » Sáb Abr 07, 2012 16:06
Priscilla Correa escreveu:![\lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p \lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p](/latexrender/pictures/a7f22620032ff7aceba3a45471e3768d.png)
Alguém pode me ajudar??
O que você escreveu é equivalente a:
![\lim_{x \to 0}\sqrt[n]{x} - \frac{\sqrt[n]{p}}{x} - p \lim_{x \to 0}\sqrt[n]{x} - \frac{\sqrt[n]{p}}{x} - p](/latexrender/pictures/92e91a908a724eb347af1b8da1846918.png)
Mas eu presumo que o exercício original seja:
![\lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} \lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p}](/latexrender/pictures/7d25615a280b19a531a71b9386e8a584.png)
Se você queria dizer isso, então deveria ter escrito algo como:
![\lim_{x \to p}\left(\sqrt[n]{x} - \sqrt[n]{p}\right)/(x - p) \lim_{x \to p}\left(\sqrt[n]{x} - \sqrt[n]{p}\right)/(x - p)](/latexrender/pictures/cc844929dacec3a3f78b5b548166555e.png)
Note a importância do uso dos parênteses! Além disso, note que x tende a p e não a 0.
Falando agora sobre a resolução desse limite, note que:
![\lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n} \lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n}](/latexrender/pictures/b4a589302a6689d509ca436dfb2a3a3e.png)
Agora use o produto notável:
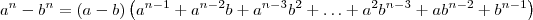
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Priscilla Correa » Sáb Abr 07, 2012 16:15
por Priscilla Correa » Sáb Abr 07, 2012 16:15
Obrigada pela resposta, eu fiquei meio confusa na hora de escrever a função e acabei digitando errado.
Então, eu resolvi e deu 1/0 (um sobre zero). Será que é isso mesmo???
-
Priscilla Correa
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Abr 07, 2012 08:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA
- Andamento: cursando
 por LuizAquino » Sáb Abr 07, 2012 16:19
por LuizAquino » Sáb Abr 07, 2012 16:19
Priscilla Correa escreveu:Obrigada pela resposta, eu fiquei meio confusa na hora de escrever a função e acabei digitando errado.
Então, eu resolvi e deu 1/0 (um sobre zero). Será que é isso mesmo???
O resultado não é esse. Envie a sua resolução para que possamos corrigi-la.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Priscilla Correa » Sáb Abr 07, 2012 16:33
por Priscilla Correa » Sáb Abr 07, 2012 16:33
Eu refiz e cheguei a outro resultado.
![\lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{}) / (x - p)
= \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{})(\sqrt[n]x + \sqrt[n]p{}{})/ (x - p)(\sqrt[n]x + \sqrt[n]p{}{})= \lim_{x \rightarrow p} 1/(\sqrt[n]x + \sqrt[n]p{}{}) = 1/(\sqrt[n]p + \sqrt[n]p{}{}) \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{}) / (x - p)
= \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{})(\sqrt[n]x + \sqrt[n]p{}{})/ (x - p)(\sqrt[n]x + \sqrt[n]p{}{})= \lim_{x \rightarrow p} 1/(\sqrt[n]x + \sqrt[n]p{}{}) = 1/(\sqrt[n]p + \sqrt[n]p{}{})](/latexrender/pictures/424b363154efd31ac8399945d56983f2.png)
Será que está certo??
-
Priscilla Correa
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Abr 07, 2012 08:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA
- Andamento: cursando
 por LuizAquino » Sáb Abr 07, 2012 16:54
por LuizAquino » Sáb Abr 07, 2012 16:54
Priscilla Correa escreveu:Eu refiz e cheguei a outro resultado.
![\lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{}) / (x - p)
= \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{})(\sqrt[n]x + \sqrt[n]p{}{})/ (x - p)(\sqrt[n]x + \sqrt[n]p{}{})= \lim_{x \rightarrow p} 1/(\sqrt[n]x + \sqrt[n]p{}{}) = 1/(\sqrt[n]p + \sqrt[n]p{}{}) \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{}) / (x - p)
= \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{})(\sqrt[n]x + \sqrt[n]p{}{})/ (x - p)(\sqrt[n]x + \sqrt[n]p{}{})= \lim_{x \rightarrow p} 1/(\sqrt[n]x + \sqrt[n]p{}{}) = 1/(\sqrt[n]p + \sqrt[n]p{}{})](/latexrender/pictures/424b363154efd31ac8399945d56983f2.png)
Será que está certo??
Está errado. O seu erro está em achar que
![\left(\sqrt[n]{x} - \sqrt[n]{p}\right)\right\left(\sqrt[n]{x} + \sqrt[n]{p}\right) \left(\sqrt[n]{x} - \sqrt[n]{p}\right)\right\left(\sqrt[n]{x} + \sqrt[n]{p}\right)](/latexrender/pictures/9b2492a0192f29c4465c28e77cea554a.png)
é igual a x - p.
Por exemplo, note que:
![\left(\sqrt[3]{x} - \sqrt[3]{p}\right)\right\left(\sqrt[3]{x} + \sqrt[3]{p}\right) = \left(\sqrt[3]{x}\right)^2 - \left(\sqrt[3]{p}\right)^2 \neq x - p \left(\sqrt[3]{x} - \sqrt[3]{p}\right)\right\left(\sqrt[3]{x} + \sqrt[3]{p}\right) = \left(\sqrt[3]{x}\right)^2 - \left(\sqrt[3]{p}\right)^2 \neq x - p](/latexrender/pictures/661d5ced03d4a6f842f7ddeee08aa636.png)
Usando o produto notável que indiquei anteriormente, temos que:
![\lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n} \lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n}](/latexrender/pictures/b4a589302a6689d509ca436dfb2a3a3e.png)
![= \lim_{x\to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{(\sqrt[n]{x} - \sqrt[n]{p})(\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1})} = \lim_{x\to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{(\sqrt[n]{x} - \sqrt[n]{p})(\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1})}](/latexrender/pictures/c19e8794a432ec461382d19217519ac7.png)
![= \lim_{x\to p}\frac{1}{\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1}} = \lim_{x\to p}\frac{1}{\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1}}](/latexrender/pictures/ec764a5d42aa7595b872abd5c8c65756.png)
Agora tente terminar o exercício.
Uma dica: para que você possa entender melhor o que acontece no caso geral, estude o que acontece em um caso particular. Por exemplo, quando n = 3 temos que:
![\lim_{x \to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x}\right)^3 - \left(\sqrt[3]{p}\right)^3} \lim_{x \to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x}\right)^3 - \left(\sqrt[3]{p}\right)^3}](/latexrender/pictures/920673a53c1c1a2ff76565584347eda7.png)
![= \lim_{x\to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x} - \sqrt[3]{p}\right)\left(\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2\right)} = \lim_{x\to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x} - \sqrt[3]{p}\right)\left(\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2\right)}](/latexrender/pictures/ab2a22f401583e947560e206556b18bd.png)
![= \lim_{x\to p}\frac{1}{\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2} = \lim_{x\to p}\frac{1}{\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2}](/latexrender/pictures/dc482690dafb549a9993a5342708e544.png)
Agora tente continuar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6650 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4796 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5128 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7270 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4446 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p \lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p](/latexrender/pictures/a7f22620032ff7aceba3a45471e3768d.png)

![\lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p \lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p](/latexrender/pictures/a7f22620032ff7aceba3a45471e3768d.png)

![\lim_{x \to 0}\sqrt[n]{x} - \frac{\sqrt[n]{p}}{x} - p \lim_{x \to 0}\sqrt[n]{x} - \frac{\sqrt[n]{p}}{x} - p](/latexrender/pictures/92e91a908a724eb347af1b8da1846918.png)
![\lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} \lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p}](/latexrender/pictures/7d25615a280b19a531a71b9386e8a584.png)
![\lim_{x \to p}\left(\sqrt[n]{x} - \sqrt[n]{p}\right)/(x - p) \lim_{x \to p}\left(\sqrt[n]{x} - \sqrt[n]{p}\right)/(x - p)](/latexrender/pictures/cc844929dacec3a3f78b5b548166555e.png)
![\lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n} \lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n}](/latexrender/pictures/b4a589302a6689d509ca436dfb2a3a3e.png)
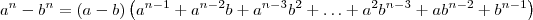



![\lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{}) / (x - p)
= \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{})(\sqrt[n]x + \sqrt[n]p{}{})/ (x - p)(\sqrt[n]x + \sqrt[n]p{}{})= \lim_{x \rightarrow p} 1/(\sqrt[n]x + \sqrt[n]p{}{}) = 1/(\sqrt[n]p + \sqrt[n]p{}{}) \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{}) / (x - p)
= \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{})(\sqrt[n]x + \sqrt[n]p{}{})/ (x - p)(\sqrt[n]x + \sqrt[n]p{}{})= \lim_{x \rightarrow p} 1/(\sqrt[n]x + \sqrt[n]p{}{}) = 1/(\sqrt[n]p + \sqrt[n]p{}{})](/latexrender/pictures/424b363154efd31ac8399945d56983f2.png)

![\left(\sqrt[n]{x} - \sqrt[n]{p}\right)\right\left(\sqrt[n]{x} + \sqrt[n]{p}\right) \left(\sqrt[n]{x} - \sqrt[n]{p}\right)\right\left(\sqrt[n]{x} + \sqrt[n]{p}\right)](/latexrender/pictures/9b2492a0192f29c4465c28e77cea554a.png) é igual a x - p.
é igual a x - p.![\left(\sqrt[3]{x} - \sqrt[3]{p}\right)\right\left(\sqrt[3]{x} + \sqrt[3]{p}\right) = \left(\sqrt[3]{x}\right)^2 - \left(\sqrt[3]{p}\right)^2 \neq x - p \left(\sqrt[3]{x} - \sqrt[3]{p}\right)\right\left(\sqrt[3]{x} + \sqrt[3]{p}\right) = \left(\sqrt[3]{x}\right)^2 - \left(\sqrt[3]{p}\right)^2 \neq x - p](/latexrender/pictures/661d5ced03d4a6f842f7ddeee08aa636.png)
![\lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n} \lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n}](/latexrender/pictures/b4a589302a6689d509ca436dfb2a3a3e.png)
![= \lim_{x\to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{(\sqrt[n]{x} - \sqrt[n]{p})(\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1})} = \lim_{x\to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{(\sqrt[n]{x} - \sqrt[n]{p})(\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1})}](/latexrender/pictures/c19e8794a432ec461382d19217519ac7.png)
![= \lim_{x\to p}\frac{1}{\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1}} = \lim_{x\to p}\frac{1}{\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1}}](/latexrender/pictures/ec764a5d42aa7595b872abd5c8c65756.png)
![\lim_{x \to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x}\right)^3 - \left(\sqrt[3]{p}\right)^3} \lim_{x \to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x}\right)^3 - \left(\sqrt[3]{p}\right)^3}](/latexrender/pictures/920673a53c1c1a2ff76565584347eda7.png)
![= \lim_{x\to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x} - \sqrt[3]{p}\right)\left(\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2\right)} = \lim_{x\to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x} - \sqrt[3]{p}\right)\left(\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2\right)}](/latexrender/pictures/ab2a22f401583e947560e206556b18bd.png)
![= \lim_{x\to p}\frac{1}{\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2} = \lim_{x\to p}\frac{1}{\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2}](/latexrender/pictures/dc482690dafb549a9993a5342708e544.png)

 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: } você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais? } você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?