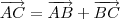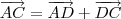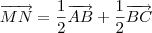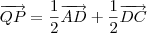por Fabio Wanderley » Qui Mar 29, 2012 20:14
por Fabio Wanderley » Qui Mar 29, 2012 20:14
Eu vim para criar um tópico, mas vou aproveitar o do colega.
Estou com muitas dificuldades em demonstrações (p. ex em GA e em Cálculo I). Como faço pra desenvolver esse tipo de raciocínio? Alguém tem algum material ou videoaula para indicar?
Desde já agradeço!
-
Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por MarceloFantini » Qui Mar 29, 2012 20:20
por MarceloFantini » Qui Mar 29, 2012 20:20
Aprender a fazer demonstrações é treino, algumas tem técnicas manjadas, você toma o jeito com o tempo. Contudo, experiências prévias (no ensino médio, como deveria ser) ajudam a compreender melhor. O primeiro livro do Gelson Iezzi da coleção Fundamentos de Matemática Elementar deve ajudar. Ele tem os rudimentos de lógica usados em matemática e dá as idéias básicas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Qui Mar 29, 2012 23:13
por LuizAquino » Qui Mar 29, 2012 23:13
Fabio Wanderley escreveu:Estou com muitas dificuldades em demonstrações (p. ex em GA e em Cálculo I). Como faço pra desenvolver esse tipo de raciocínio? Alguém tem algum material ou videoaula para indicar?
Além do que o colega
MarceloFantini falou, vide também o que foi discutido no tópico abaixo:
Dificuldade em exercícios de demonstraçãoviewtopic.php?f=120&t=7037
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Wanderley » Sex Mar 30, 2012 13:15
por Fabio Wanderley » Sex Mar 30, 2012 13:15
Obrigado, Marcelo e Luiz!
Já estou pesquisando o material. Vou fazer os treinos.
Meu objetivo é verificar uma conjectura que meu professor de GA passou. É mais ou menos isso: "Dado um quadrilátero qualquer, tomam-se os pontos médios de cada lado. Estes serão os vértices de um paralelogramo."
Espero conseguir e postar aqui no fórum

-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por LuizAquino » Sex Mar 30, 2012 15:09
por LuizAquino » Sex Mar 30, 2012 15:09
Fabio Wanderley escreveu:Meu objetivo é verificar uma conjectura que meu professor de GA passou. É mais ou menos isso: "Dado um quadrilátero qualquer, tomam-se os pontos médios de cada lado. Estes serão os vértices de um paralelogramo."
Eu presumo que o objetivo seja provar essa proposição usando vetores. Eu vou mostrar a ideia e você tenta fazer o exercício.
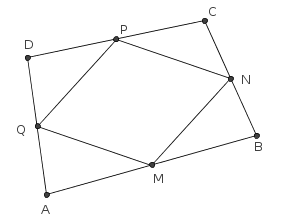
Considere o quadrilátero ABCD ilustrado na figura abaixo. Tome os pontos médios M, N, P e Q, respectivamente, dos lados AB, BC, CD e DA.
- figura1.png (8.02 KiB) Exibido 945 vezes
Para provar que o quadrilátero MNPQ é um paralologramo, você precisa provar que o lado MN é paralelo ao lado PQ e o lado NP é paralelo ao lado QM.
Considere a figura abaixo. Observe os vetores

,
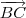
,
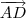
,

,
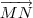
,
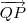
e
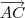
.
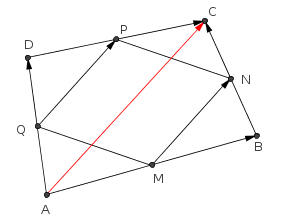
- figura2.png (7.52 KiB) Exibido 945 vezes
Note as seguintes relações:
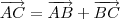
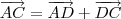
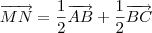
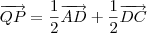
Agora responda: o que você pode concluir dessas relações?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Wanderley » Sex Abr 06, 2012 13:38
por Fabio Wanderley » Sex Abr 06, 2012 13:38
LuizAquino escreveu:Fabio Wanderley escreveu:Meu objetivo é verificar uma conjectura que meu professor de GA passou. É mais ou menos isso: "Dado um quadrilátero qualquer, tomam-se os pontos médios de cada lado. Estes serão os vértices de um paralelogramo."
Eu presumo que o objetivo seja provar essa proposição usando vetores. Eu vou mostrar a ideia e você tenta fazer o exercício.
Considere o quadrilátero ABCD ilustrado na figura abaixo. Tome os pontos médios M, N, P e Q, respectivamente, dos lados AB, BC, CD e DA.
figura1.png
Para provar que o quadrilátero MNPQ é um paralologramo, você precisa provar que o lado MN é paralelo ao lado PQ e o lado NP é paralelo ao lado QM.
Considere a figura abaixo. Observe os vetores

,
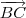
,
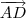
,

,
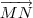
,
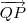
e
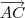
.
figura2.png
Note as seguintes relações:
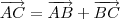
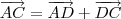
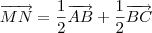
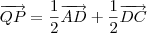
Agora responda: o que você pode concluir dessas relações?
Observei que os vetores MN e QP é 1/2, cada um, do vetor AC. Com isso conclui que eles (MN e QP) são paralelos. Logo o quadrilatero MNPQ é um paralelogramo.
Obrigado!
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por LuizAquino » Sex Abr 06, 2012 19:02
por LuizAquino » Sex Abr 06, 2012 19:02
Fabio Wanderley escreveu:Observei que os vetores MN e QP é 1/2, cada um, do vetor AC. Com isso conclui que eles (MN e QP) são paralelos.
Ok.
Fabio Wanderley escreveu:Logo o quadrilatero MNPQ é um paralelogramo.
Calma! Você ainda não pode concluir isso. Você precisa antes provar que o lado NP é paralelo ao lado QM. Tente fazer essa parte.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- DEMONSTRAÇÃO
por arima » Seg Nov 08, 2010 08:40
- 8 Respostas
- 5637 Exibições
- Última mensagem por roseli

Qua Nov 10, 2010 21:03
Álgebra Elementar
-
- Demonstração
por Lorettto » Qui Dez 16, 2010 23:03
- 3 Respostas
- 2120 Exibições
- Última mensagem por Elcioschin

Seg Dez 20, 2010 12:39
Álgebra Elementar
-
- Demonstração
por Pedro2 » Sáb Mar 12, 2011 15:38
- 1 Respostas
- 1839 Exibições
- Última mensagem por Guill

Sex Abr 20, 2012 16:01
Matrizes e Determinantes
-
- PA - Demonstração
por jessicaccs » Sex Mar 25, 2011 11:52
- 1 Respostas
- 1363 Exibições
- Última mensagem por Elcioschin

Sex Mar 25, 2011 14:55
Progressões
-
- Demonstração
por tigre matematico » Dom Nov 06, 2011 12:05
- 0 Respostas
- 1004 Exibições
- Última mensagem por tigre matematico

Dom Nov 06, 2011 12:05
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 ,
, 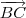 ,
, 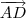 ,
,  ,
, 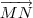 ,
, 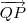 e
e 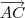 .
.