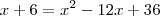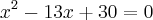Interpretação dessa questão

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Interpretação dessa questão

Regras do fórum
Responder

Interpretação dessa questão

Mensagempor Joelson » Dom Jun 21, 2009 17:22

Sei que aresposta é 10, porém como montar a questão? Desculpem se me deu branco.
(UFSM) A idade que Genoveva terá daqui a 6 anos será igual ao quadrado da idade que tinha há 6 anos. A idade de Genoveva é:

Alguém consegue a solução p mim?

Tentei p báskara usando x+6=(x-6) ao quadrado , mas não deu.
`´E só um exercício da minha filha p o colégio. Que coisa!!
Faz tempo essa matéria. Preciso reciclar.
Alguém me ajuda?
Joelson
Novo Usuário
Novo Usuário
 
Mensagens: 2
Registrado em: Dom Jun 21, 2009 16:42
Formação Escolar: ENSINO MÉDIO
Andamento: formado
Voltar ao topo

Re: Interpretação dessa questão

Mensagempor ginrj » Dom Jun 21, 2009 18:36

seu raciocinio esta certo, a resolução é

x+6=x-6{}^{2}
x+6=x{}^{2}-12x+36
x{}^{2} -13x+30=0

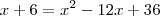
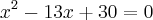
as raizes dessa equação são 10 e 3, logo so podemos usar o 10 como resposta.
Resposta 10
Os números governam o Universo
ginrj
Usuário Dedicado
Usuário Dedicado
 
Mensagens: 37
Registrado em: Sex Mar 06, 2009 18:28
Localização: Rio de Janeiro
Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
Área/Curso: Pré.Militar
Andamento: cursando
Voltar ao topo

Re: Interpretação dessa questão

Mensagempor Joelson » Dom Jun 21, 2009 19:13

ginrj escreveu:seu raciocinio esta certo, a resolução é

x+6=x-6{}^{2}
x+6=x{}^{2}-12x+36
x{}^{2} -13x+30=0

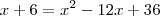
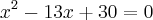
as raizes dessa equação são 10 e 3, logo so podemos usar o 10 como resposta.
Resposta 10



Valeu mesmo!!!
Nossa como eu pude voar nela!!!
Joelson
Novo Usuário
Novo Usuário
 
Mensagens: 2
Registrado em: Dom Jun 21, 2009 16:42
Formação Escolar: ENSINO MÉDIO
Andamento: formado
Voltar ao topo
Responder

Voltar para Álgebra Elementar

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum