 por Arthur_Bulcao » Seg Abr 02, 2012 17:27
por Arthur_Bulcao » Seg Abr 02, 2012 17:27
Mais uma vez, eu com dúvidas.
Sem usar L'Hospital, poderiam me ajudar a resolver:
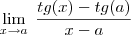
Não tenho a mínima noção de como começar.
Obrigado.
Editado pela última vez por
Arthur_Bulcao em Seg Abr 02, 2012 18:04, em um total de 1 vez.
-
Arthur_Bulcao
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sex Mar 23, 2012 17:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Graduação em Engenharia Acústica
- Andamento: cursando
 por Arthur_Bulcao » Seg Abr 02, 2012 18:04
por Arthur_Bulcao » Seg Abr 02, 2012 18:04
Saquei!!
Lembrei que
![tg(a-b)=\frac{\emph{tg(a)-tg(b)}}{1+tg(a).tg(b)}\;\Rightarrow\\\;\emph{tg(a)-tg(b)}=tg(a-b).[1+tg(a).tg(b)] tg(a-b)=\frac{\emph{tg(a)-tg(b)}}{1+tg(a).tg(b)}\;\Rightarrow\\\;\emph{tg(a)-tg(b)}=tg(a-b).[1+tg(a).tg(b)]](/latexrender/pictures/95913122803ae5346390117d9128ea08.png)
e dá pra substituir:
![\lim_{x\rightarrow a}\;\frac{\emph{tg(x)-tg(a)}}{x-a} \Rightarrow Substituindo \Rightarrow\,\lim_{x\rightarrow a}\;\frac{\emph{tg(a-b).[1+tg(a).tg(b)]}}{x-a} \lim_{x\rightarrow a}\;\frac{\emph{tg(x)-tg(a)}}{x-a} \Rightarrow Substituindo \Rightarrow\,\lim_{x\rightarrow a}\;\frac{\emph{tg(a-b).[1+tg(a).tg(b)]}}{x-a}](/latexrender/pictures/a1728a6e541512224ef683e480446c68.png)
Usando uma das propriedades de limites, temos:
![\lim_{x\rightarrow a}\;\frac{tg(a-b)}{x-a}\,.\,\lim_{x\rightarrow a}[1+tg(a).tg(b)] \lim_{x\rightarrow a}\;\frac{tg(a-b)}{x-a}\,.\,\lim_{x\rightarrow a}[1+tg(a).tg(b)]](/latexrender/pictures/ba70b27c381a68f14ec3fefda3a5f603.png)
Em suma, o resultado é
![\lim_{x\rightarrow a}\;\frac{tg(a-b)}{x-a}\,.\,\lim_{x\rightarrow a}[1+tg(a).tg(b)]\:=\:sec^2a \lim_{x\rightarrow a}\;\frac{tg(a-b)}{x-a}\,.\,\lim_{x\rightarrow a}[1+tg(a).tg(b)]\:=\:sec^2a](/latexrender/pictures/8ebd54fed9d90885581913897ce836db.png)
-
Arthur_Bulcao
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sex Mar 23, 2012 17:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Graduação em Engenharia Acústica
- Andamento: cursando
 por MarceloFantini » Seg Abr 02, 2012 19:28
por MarceloFantini » Seg Abr 02, 2012 19:28
Sua resolução está mal escrita. Primeiro, você esqueceu de trocar o b por x, segundo, você não mostrou porque
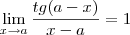
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Adição e Subtração.
por re999mat » Qui Ago 09, 2018 17:01
- 0 Respostas
- 3509 Exibições
- Última mensagem por re999mat

Qui Ago 09, 2018 17:01
Álgebra Elementar
-
- Subtração de modulos, em uma inequação
por ferrazrafael » Qua Set 01, 2010 15:35
- 1 Respostas
- 3902 Exibições
- Última mensagem por MarceloFantini

Qua Set 01, 2010 20:52
Funções
-
- Adição e Subtração de Frações
 por LuizCarlos » Sáb Mar 17, 2012 00:10
por LuizCarlos » Sáb Mar 17, 2012 00:10
- 1 Respostas
- 3902 Exibições
- Última mensagem por fraol

Sáb Mar 17, 2012 11:58
Álgebra Elementar
-
- Adição e Subtração de Arcos.
por DPeres » Sáb Mai 05, 2012 02:13
- 3 Respostas
- 2910 Exibições
- Última mensagem por LuizAquino

Dom Mai 06, 2012 09:05
Trigonometria
-
- Adição e Subtração de Arcos.
por DPeres » Sáb Mai 05, 2012 02:18
- 1 Respostas
- 1776 Exibições
- Última mensagem por LuizAquino

Sáb Mai 05, 2012 10:44
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![tg(a-b)=\frac{\emph{tg(a)-tg(b)}}{1+tg(a).tg(b)}\;\Rightarrow\\\;\emph{tg(a)-tg(b)}=tg(a-b).[1+tg(a).tg(b)] tg(a-b)=\frac{\emph{tg(a)-tg(b)}}{1+tg(a).tg(b)}\;\Rightarrow\\\;\emph{tg(a)-tg(b)}=tg(a-b).[1+tg(a).tg(b)]](/latexrender/pictures/95913122803ae5346390117d9128ea08.png)
![\lim_{x\rightarrow a}\;\frac{\emph{tg(x)-tg(a)}}{x-a} \Rightarrow Substituindo \Rightarrow\,\lim_{x\rightarrow a}\;\frac{\emph{tg(a-b).[1+tg(a).tg(b)]}}{x-a} \lim_{x\rightarrow a}\;\frac{\emph{tg(x)-tg(a)}}{x-a} \Rightarrow Substituindo \Rightarrow\,\lim_{x\rightarrow a}\;\frac{\emph{tg(a-b).[1+tg(a).tg(b)]}}{x-a}](/latexrender/pictures/a1728a6e541512224ef683e480446c68.png)
![\lim_{x\rightarrow a}\;\frac{tg(a-b)}{x-a}\,.\,\lim_{x\rightarrow a}[1+tg(a).tg(b)] \lim_{x\rightarrow a}\;\frac{tg(a-b)}{x-a}\,.\,\lim_{x\rightarrow a}[1+tg(a).tg(b)]](/latexrender/pictures/ba70b27c381a68f14ec3fefda3a5f603.png)
![\lim_{x\rightarrow a}\;\frac{tg(a-b)}{x-a}\,.\,\lim_{x\rightarrow a}[1+tg(a).tg(b)]\:=\:sec^2a \lim_{x\rightarrow a}\;\frac{tg(a-b)}{x-a}\,.\,\lim_{x\rightarrow a}[1+tg(a).tg(b)]\:=\:sec^2a](/latexrender/pictures/8ebd54fed9d90885581913897ce836db.png)

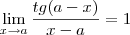 .
.


 .
.



