 por Guilhermme » Sáb Mar 31, 2012 17:06
por Guilhermme » Sáb Mar 31, 2012 17:06
dados A (1,0), B (4,1) e C(4,y), calcule y de modo que se tenha BÂC = 60º
tenho certeza q
ate aqui esta certo pois a professora me ajudou, só q tem prova segunda e eu preciso saber como se faz, como eu continuo isso :
324+72y+4y² = 90+10y² a resposta vai dar
![y= mais e menos 5\sqrt[]{3} y= mais e menos 5\sqrt[]{3}](/latexrender/pictures/c0b31de0b8f92572070f6f99206de280.png)
-
Guilhermme
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mar 24, 2012 18:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Sáb Mar 31, 2012 19:49
por LuizAquino » Sáb Mar 31, 2012 19:49
Guilhermme escreveu:dados A (1,0), B (4,1) e C(4,y), calcule y de modo que se tenha BÂC = 60º
tenho certeza q
ate aqui esta certo pois a professora me ajudou, só q tem prova segunda e eu preciso saber como se faz, como eu continuo isso :
324+72y+4y² = 90+10y² a resposta vai dar
![y= mais e menos 5\sqrt[]{3} y= mais e menos 5\sqrt[]{3}](/latexrender/pictures/c0b31de0b8f92572070f6f99206de280.png)
Isso é uma equação polinomial do segundo grau.
Você pode arrumá-la como:
6y² - 72y - 234 = 0
Agora basta resolvê-la.
Se você não sabe como resolver essa equação, então eu recomendo que você assista a videoaula "Matemática Zero - Aula 14 - Equação do Segundo Grau". Ela está disponível no canal do Nerckie no YouTube:
http://www.youtube.com/nerckie
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jeissond » Ter Abr 17, 2012 23:49
por jeissond » Ter Abr 17, 2012 23:49
LuizAquino escreveu:Guilhermme escreveu:dados A (1,0), B (4,1) e C(4,y), calcule y de modo que se tenha BÂC = 60º
tenho certeza q
ate aqui esta certo pois a professora me ajudou, só q tem prova segunda e eu preciso saber como se faz, como eu continuo isso :
324+72y+4y² = 90+10y² a resposta vai dar
![y= mais e menos 5\sqrt[]{3} y= mais e menos 5\sqrt[]{3}](/latexrender/pictures/c0b31de0b8f92572070f6f99206de280.png)
Isso é uma equação polinomial do segundo grau.
Você pode arrumá-la como:
6y² - 72y - 234 = 0
Agora basta resolvê-la.
Se você não sabe como resolver essa equação, então eu recomendo que você assista a videoaula "Matemática Zero - Aula 14 - Equação do Segundo Grau". Ela está disponível no canal do Nerckie no YouTube:
http://www.youtube.com/nerckie
Amigos, tenho prova amanhã, CVGA, e to batendo cabeça para resolver esta questão... não consigo nem sair do enunciado, alguém poderia me ajudar com ela é exatamente a mesma questão e dados!
-
jeissond
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Abr 17, 2012 23:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Ambiental
- Andamento: cursando
 por LuizAquino » Qua Abr 18, 2012 15:41
por LuizAquino » Qua Abr 18, 2012 15:41
jeissond escreveu:Amigos, tenho prova amanhã, CVGA, e to batendo cabeça para resolver esta questão... não consigo nem sair do enunciado, alguém poderia me ajudar com ela é exatamente a mesma questão e dados!
Você já deve ter estudado que se

é o ângulo formado entre os vetores
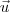
e

, então temos que:
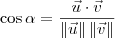
Pelos dados do exercício, temos que BÂC = 60º. Portanto, podemos dizer que:
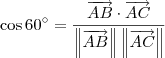
Usando os outros dados do exercício, temos que:
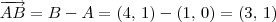
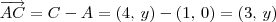
Agora tente continuar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nico Romani » Qui Mar 31, 2016 17:01
por Nico Romani » Qui Mar 31, 2016 17:01
Apos voce simplificar essa equçao de segundo grau: y(ao quadrado) -12y -39, voce faz a baskara: y= 12+/- raiz de 300 dividido por 2, raiz de 300 é igual a 10raiz de 3,logo, é so dividir o 12 por 2 ficando 6, e o 10 na frente da raiz por 2 tbm, a resposta final é : y=6+/- 5raiz de 3
-
Nico Romani
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mar 31, 2016 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng.Civil
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- P.G., calcule Sn=9+99+999... +10n-1
por georgefdfdl » Qui Nov 10, 2011 23:49
- 1 Respostas
- 1631 Exibições
- Última mensagem por LuizAquino

Sex Nov 11, 2011 17:41
Progressões
-
- Calcule a e b
por andersontricordiano » Dom Mar 02, 2014 12:01
- 3 Respostas
- 4678 Exibições
- Última mensagem por nat-larissa

Seg Mar 03, 2014 20:12
Sistemas de Equações
-
- Calcule
por andersontricordiano » Ter Mar 18, 2014 00:34
- 1 Respostas
- 2006 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 06, 2016 11:38
Aritmética
-
- Calcule f(x)
por kjelin » Ter Fev 02, 2016 01:39
- 1 Respostas
- 2721 Exibições
- Última mensagem por DanielFerreira

Seg Fev 08, 2016 16:47
Cálculo: Limites, Derivadas e Integrais
-
- Calcule o 1º termo
 por Cleyson007 » Dom Dez 27, 2009 13:47
por Cleyson007 » Dom Dez 27, 2009 13:47
- 1 Respostas
- 2052 Exibições
- Última mensagem por Lucio Carvalho

Seg Dez 28, 2009 09:46
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![y= mais e menos 5\sqrt[]{3} y= mais e menos 5\sqrt[]{3}](/latexrender/pictures/c0b31de0b8f92572070f6f99206de280.png)

![y= mais e menos 5\sqrt[]{3} y= mais e menos 5\sqrt[]{3}](/latexrender/pictures/c0b31de0b8f92572070f6f99206de280.png)



 é o ângulo formado entre os vetores
é o ângulo formado entre os vetores 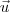 e
e  , então temos que:
, então temos que: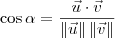
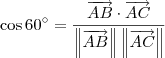
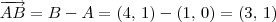
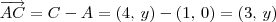



 .
.



