 por Kabection » Qui Mar 29, 2012 22:20
por Kabection » Qui Mar 29, 2012 22:20
queria uma ajuda para conseguir fatorar esse limite, o unico modo que consigo para resolver, é usando a tabela de valores próximos do x usando calculadora. Alguém sabe fazer de outro modo?
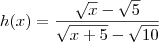
se x for diferente de 5,
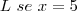
Usando a tabela calculando valores próximos a resposta dá 1,4142 =
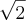
.
-
Kabection
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jan 16, 2012 15:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por LuizAquino » Sex Mar 30, 2012 02:21
por LuizAquino » Sex Mar 30, 2012 02:21
Kabection escreveu:queria uma ajuda para conseguir fatorar esse limite, o unico modo que consigo para resolver, é usando a tabela de valores próximos do x usando calculadora. Alguém sabe fazer de outro modo?
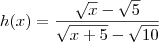
se x for diferente de 5,
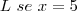
Usando a tabela calculando valores próximos a resposta dá 1,4142 =
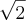
.
DicaMultiplique o numerador e o denominador por
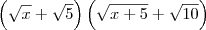
:
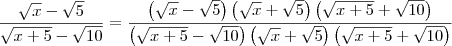
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Kabection » Sex Mar 30, 2012 22:38
por Kabection » Sex Mar 30, 2012 22:38
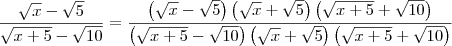
Fica:
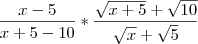
Cortando (x-5) com (x+5-10) fica:
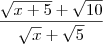
Substituindo x=5 fica:
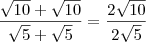
Cortando 2 e usando a propriedade da divisão das raízes:
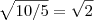
Valeu Luiz Aquino.
-
Kabection
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jan 16, 2012 15:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
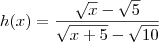 se x for diferente de 5,
se x for diferente de 5, 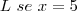
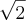 .
.
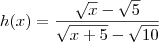 se x for diferente de 5,
se x for diferente de 5, 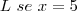
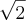 .
.
se x for diferente de 5,
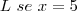
.
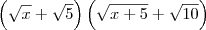 :
: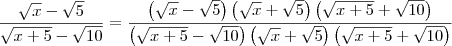

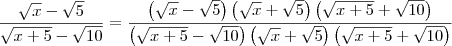
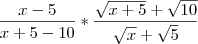

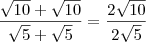
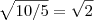

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.