 por joaofonseca » Sex Mar 30, 2012 12:59
por joaofonseca » Sex Mar 30, 2012 12:59
Seja este limite:
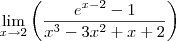
Já tentei mudar a variável:
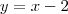
, deste modo quando
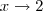
,
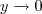
. Mas não consegui chegar ao limite especial, que a expressão sugere.
Que alteração de variável tenho de fazer?
Obrigado
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por joaofonseca » Sáb Mar 31, 2012 11:15
por joaofonseca » Sáb Mar 31, 2012 11:15
Obrigado pela ajuda
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resolver limite de exponencial por L'Hospital.
 por Sobreira » Sáb Nov 30, 2013 15:00
por Sobreira » Sáb Nov 30, 2013 15:00
- 9 Respostas
- 6588 Exibições
- Última mensagem por e8group

Sáb Nov 30, 2013 17:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Não sei como Resolver
por eli83 » Qua Out 10, 2012 09:48
- 7 Respostas
- 3200 Exibições
- Última mensagem por MrJuniorFerr

Qua Out 10, 2012 23:22
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver limite?
por raquelzinha72 » Dom Jun 05, 2016 08:32
- 1 Respostas
- 2705 Exibições
- Última mensagem por Cleyson007

Dom Jun 05, 2016 10:57
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver esse limite?
por samra » Sáb Mar 31, 2012 02:38
- 4 Respostas
- 3544 Exibições
- Última mensagem por fraol

Dom Abr 01, 2012 14:56
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver esse limite?
por duborgis » Sex Abr 06, 2012 13:29
- 12 Respostas
- 7791 Exibições
- Última mensagem por Fabio Wanderley

Dom Abr 08, 2012 16:04
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
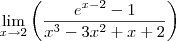
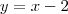 , deste modo quando
, deste modo quando 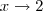 ,
, 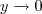 . Mas não consegui chegar ao limite especial, que a expressão sugere.
. Mas não consegui chegar ao limite especial, que a expressão sugere.
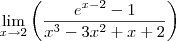
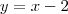 , deste modo quando
, deste modo quando 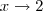 ,
, 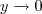 . Mas não consegui chegar ao limite especial, que a expressão sugere.
. Mas não consegui chegar ao limite especial, que a expressão sugere.
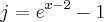
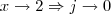

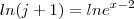
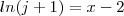
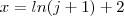
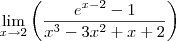
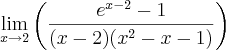
![\lim_{j \to 0}\left(\frac{j}{[ln(j+1)+2-2].([ln(j+1)+2]^2-[ln(j+1)+2]-1)}\right) \lim_{j \to 0}\left(\frac{j}{[ln(j+1)+2-2].([ln(j+1)+2]^2-[ln(j+1)+2]-1)}\right)](/latexrender/pictures/aa20c39fafc5308790cbe1fa42935b18.png)
![\lim_{j \to 0}{\left(\frac{[ln(j+1)].([ln(j+1)+2]^2-[ln(j+1)+2]-1)}{j}\right)}^{-1} \lim_{j \to 0}{\left(\frac{[ln(j+1)].([ln(j+1)+2]^2-[ln(j+1)+2]-1)}{j}\right)}^{-1}](/latexrender/pictures/a22781fbd632677a6dc13315acd763aa.png)
![{\left(\lim_{j \to 0}\frac{1}{j}.ln(j+1).\lim_{j \to 0}([ln(j+1)+2]^2-[ln(j+1)+2]-1)\right)}^{-1} {\left(\lim_{j \to 0}\frac{1}{j}.ln(j+1).\lim_{j \to 0}([ln(j+1)+2]^2-[ln(j+1)+2]-1)\right)}^{-1}](/latexrender/pictures/ebd2602cbba315ebaac45a903e0ea17d.png)
![{\left(\lim_{j \to 0}{ln(j+1)}^{\frac{1}{j}}.\lim_{j \to 0}([ln(j+1)+2]^2-[ln(j+1)+2]-1)\right)}^{-1} {\left(\lim_{j \to 0}{ln(j+1)}^{\frac{1}{j}}.\lim_{j \to 0}([ln(j+1)+2]^2-[ln(j+1)+2]-1)\right)}^{-1}](/latexrender/pictures/ebe991a49078279310be00f89308abbc.png)
![{\left(ln\left(\lim_{j \to 0}{(j+1)}^{\frac{1}{j}}\right).\lim_{j \to 0}([ln(j+1)+2]^2-[ln(j+1)+2]-1)\right)}^{-1} {\left(ln\left(\lim_{j \to 0}{(j+1)}^{\frac{1}{j}}\right).\lim_{j \to 0}([ln(j+1)+2]^2-[ln(j+1)+2]-1)\right)}^{-1}](/latexrender/pictures/63f8dd07b530dd25df2306dbcbab760f.png)
![{\left(ln\left(e\right).([ln(0+1)+2]^2-[ln(0+1)+2]-1)\right)}^{-1} {\left(ln\left(e\right).([ln(0+1)+2]^2-[ln(0+1)+2]-1)\right)}^{-1}](/latexrender/pictures/374ed7e8724f14f500ceb1aecddac7cf.png)
![{(1.([0+2]^2-[0+2]-1))}^{-1} {(1.([0+2]^2-[0+2]-1))}^{-1}](/latexrender/pictures/191c2b781b797fc9232e6dfb31ab4183.png)
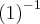



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.