 por JessyBr » Qui Mar 29, 2012 00:46
por JessyBr » Qui Mar 29, 2012 00:46
Amanha tenho prova de elementos de calculo e não estou conseguindo resolver alguns exercícios da revisão!
Sei calcular a maxima e minima de f(x) e usar os testes de derivada mas o mais simples como obter as raizes da função eu nao consigo!
a questão:
1. Determine os intervalos em que f(x) é crescente e decrescente, os valores de máximo e mínimo relativos de f(x), os intervalos de concavidade, os pontos de inflexão e o gráfico de f(x) utilizando os testes da 1a e da 2a derivada:
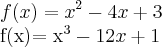
Eu queria ajuda para determinar os intervalos de f(x), mas por favor coloquem a evolucao dos calculos pois não sei fazê-los!
Obrigadaa

-
JessyBr
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mar 29, 2012 00:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: arquitetura
- Andamento: cursando
 por MarceloFantini » Qui Mar 29, 2012 10:50
por MarceloFantini » Qui Mar 29, 2012 10:50
Mostre o seu desenvolvimento para que possamos identificar onde você está tendo problemas. Assim, entenderá seus possíveis erros e aprenderá melhor.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Qui Mar 29, 2012 12:41
por LuizAquino » Qui Mar 29, 2012 12:41
JessyBr escreveu:Sei calcular a maxima e minima de f(x) e usar os testes de derivada mas o mais simples como obter as raizes da função eu nao consigo!
a questão:
1. Determine os intervalos em que f(x) é crescente e decrescente, os valores de máximo e mínimo relativos de f(x), os intervalos de concavidade, os pontos de inflexão e o gráfico de f(x) utilizando os testes da 1a e da 2a derivada:
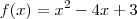

Em ambos os casos, você vai precisar determinar as raízes da equação:
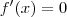
.
Para a primeira função do exercício, após derivar você terá que resolver uma equação polinomial do primeiro grau. Já para a segunda função, após derivar você terá que resolver uma equação polinomial do segundo grau.
Para saber como resolver esses tipos de equação, eu recomendo que você assista as videoaulas "Matemática Zero - Aula 13 - Equação do Primeiro Grau" e "Matemática Zero - Aula 14 - Equação do Segundo Grau". Elas estão disponíveis no canal do Nerckie no YouTube:
http://www.youtube.com/nerckieApós assistir essas videoaulas tente resolver o exercício. Caso ainda tenha dúvidas, mostre o seu desenvolvimento assim como já sugeriu o colega
MarceloFantini.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcular intervalos de crescimento e decrescimento da função
por Eduardooitavo » Sáb Jun 09, 2012 18:06
- 1 Respostas
- 2534 Exibições
- Última mensagem por MarceloFantini

Sáb Jun 09, 2012 19:32
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2265 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] como calcular
por ma-mine » Sáb Jul 13, 2013 15:24
- 3 Respostas
- 2521 Exibições
- Última mensagem por e8group

Dom Jul 14, 2013 19:00
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] como calcular
por ghiza » Dom Jul 14, 2013 21:45
- 2 Respostas
- 1774 Exibições
- Última mensagem por Man Utd

Dom Jul 14, 2013 23:39
Cálculo: Limites, Derivadas e Integrais
-
- Como calcular derivadas com a constante "e"
por fer_carnie » Seg Jun 20, 2011 20:40
- 1 Respostas
- 2095 Exibições
- Última mensagem por Fabio Cabral

Seg Jun 20, 2011 22:22
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
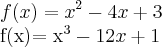





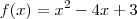

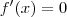 .
.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.