 por FelipeTURBO » Sex Mar 23, 2012 23:26
por FelipeTURBO » Sex Mar 23, 2012 23:26
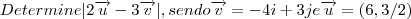
Achei milhares de resultados e não consigo saber qual o correto.
-
FelipeTURBO
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 23, 2012 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por MarceloFantini » Sáb Mar 24, 2012 07:57
por MarceloFantini » Sáb Mar 24, 2012 07:57
Felipe, procure mostrar seu desenvolvimento. Primeiramente, qual foi seu resultado de

?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por FelipeTURBO » Dom Mar 25, 2012 01:09
por FelipeTURBO » Dom Mar 25, 2012 01:09
Determine

, eu achei no
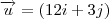
, pois multipliquei por 2.
E no
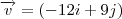
, multipliquei por 3. E depois fiz a subtração dos dois
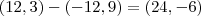
E após esse processo fiz o modulo
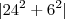
que resultou em
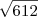
Gostaria de saber se fiz certo ou se errei, pois achei outros valores após achar que estava errado pelo tamanho do número,
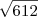
.
-
FelipeTURBO
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 23, 2012 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por MarceloFantini » Dom Mar 25, 2012 13:20
por MarceloFantini » Dom Mar 25, 2012 13:20
Está correto, todo o processo e a resposta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [VETORES]Alguém me ajuda com vetores?
por LAZAROTTI » Seg Set 17, 2012 00:49
- 2 Respostas
- 7372 Exibições
- Última mensagem por young_jedi

Seg Set 17, 2012 11:28
Geometria Analítica
-
- [Vetores] Módulo e Versor de vetores
por LAZAROTTI » Sáb Set 22, 2012 22:42
- 1 Respostas
- 2991 Exibições
- Última mensagem por young_jedi

Sáb Set 22, 2012 22:50
Geometria Analítica
-
- [Vetores] Produto Entre Vetores
por _bruno94 » Qua Jul 10, 2013 00:34
- 1 Respostas
- 5214 Exibições
- Última mensagem por temujin

Qua Jul 10, 2013 14:27
Geometria Analítica
-
- [Vetores] Vetores iguais
por KleinIll » Dom Nov 04, 2012 12:17
- 2 Respostas
- 3407 Exibições
- Última mensagem por KleinIll

Dom Nov 04, 2012 13:50
Geometria Analítica
-
- [Vetores] Operações com vetores
por IlgssonBraga » Qui Jul 18, 2013 11:42
- 1 Respostas
- 2383 Exibições
- Última mensagem por Russman

Qui Jul 18, 2013 15:45
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
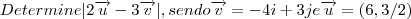

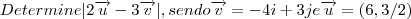

 ?
?

 , eu achei no
, eu achei no 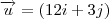 , pois multipliquei por 2.
, pois multipliquei por 2.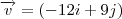 , multipliquei por 3. E depois fiz a subtração dos dois
, multipliquei por 3. E depois fiz a subtração dos dois 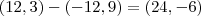
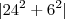 que resultou em
que resultou em 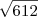
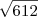 .
.
