 por thiagodr » Sex Mar 23, 2012 01:07
por thiagodr » Sex Mar 23, 2012 01:07

Suponha que o valor da demanda mostrada no gráfico em2003 corresponda a janeiro de 2003 e que, nos 24 meses seguintes, entre 2003 e 2005, a demanda tenha crescido em progressão aritmética até atingir o valor correspondente a 2005. Pode-se concluir, então, que em outubro de 2003 a demanda era superior a 1.735 mbpd.
-------------------
Eu fiz:
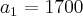
e
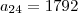
logo,
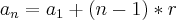
==>

==>
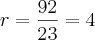
e
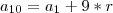
==>
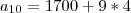
==>
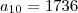
resposta é CERTA.
porém ela é errada!
no gabarito diz: alterado de C para E. A razão da P.A. r = 3,833 e
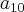
=
1.700 + 9 × 3,833 < 1.735
alguém pode me explicar por que ele fez a razão como sendo 92/24 e não o 92/23?
-
thiagodr
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Mar 23, 2012 00:52
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: mestrado em Engenharia Nuclear
- Andamento: cursando
 por DanielFerreira » Sex Mar 23, 2012 23:28
por DanielFerreira » Sex Mar 23, 2012 23:28
Eu resolveria assim:
a1 = 1700
a24 = 1792
a10 = ?
a24 = a1 + 23r
1792 = 1700 + 23r
23r = 92
r = 4
a10 = a1 + 9r
a10 = 1700 + 9 . 4
a10 = 1736
Certa!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por thiagodr » Sex Mar 23, 2012 23:35
por thiagodr » Sex Mar 23, 2012 23:35
Foi exatamente isto que eu fiz! A minha duvida é por que a Cespe disse que este raciocínio está errado, com aquela justificativa.
O gabarito lançado erá: C.
depois eles retificaram e lançaram esta justificativa: alterado de C para E. A razão da P.A. r = 3,833 e
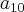
= 1.700 + 9 × 3,833 < 1.735
-
thiagodr
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Mar 23, 2012 00:52
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: mestrado em Engenharia Nuclear
- Andamento: cursando
 por thiagodr » Sáb Abr 07, 2012 16:34
por thiagodr » Sáb Abr 07, 2012 16:34
bem, o único modo dela dar o resultado do gabarito é se considerarmos que vai de janeiro a janeiro e não de janeiro a dezembro.
deste modo a resposta concorda com o gabarito.
-
thiagodr
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Mar 23, 2012 00:52
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: mestrado em Engenharia Nuclear
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Concurso Petrobras
 por lourivallobo » Ter Jan 24, 2012 20:47
por lourivallobo » Ter Jan 24, 2012 20:47
- 1 Respostas
- 3963 Exibições
- Última mensagem por LuizAquino

Ter Jan 24, 2012 21:12
Logaritmos
-
- Concurso Petrobras
por lourivallobo » Ter Jan 24, 2012 20:49
- 1 Respostas
- 1451 Exibições
- Última mensagem por LuizAquino

Ter Jan 24, 2012 21:51
Estatística
-
- Concurso Petrobras
por lourivallobo » Ter Jan 24, 2012 20:52
- 1 Respostas
- 3018 Exibições
- Última mensagem por LuizAquino

Ter Jan 24, 2012 22:08
Estatística
-
- Concurso Petrobras
 por lourivallobo » Qua Jan 25, 2012 09:13
por lourivallobo » Qua Jan 25, 2012 09:13
- 4 Respostas
- 2994 Exibições
- Última mensagem por Arkanus Darondra

Qua Jan 25, 2012 17:30
Matrizes e Determinantes
-
- DERIVADA - CONCURSO PETROBRAS
por pinkfluor » Qua Mar 02, 2011 11:10
- 2 Respostas
- 2328 Exibições
- Última mensagem por LuizAquino

Qua Mar 02, 2011 12:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

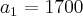 e
e 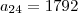
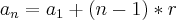 ==>
==>  ==>
==> 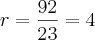
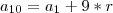 ==>
==> 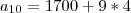 ==>
==>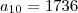
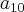 =
= 



 .
.



