Pri Ferreira escreveu:Considere-se o conjunto A = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11;
12; 13; 14}, formado pelos quatorze primeiros inteiros positivos,
e um conjunto B, formado por todos os subconjuntos
de A com exatamente três elementos. Escolhendo-se
aleatoriamente um elemento do conjunto B, a probabilidade
de ele ser formado por três números cuja soma é um múltiplo
de 3 equivale a:
a)168/17
b)4/31
c)1/13
d)31/91
Note que cada
elemento do conjunto B tem o formato {a, b, c}.
Note também que o número de elementos de B será
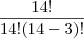
.
Agora você precisa listar todos os elementos de B que são formados por três números cuja a soma é um múltiplo de 3. Veja alguns exemplos: {1, 2, 3}, {1, 2, 6}, {1, 3, 5}, etc.
Depois que você contar quantos elementos tem nessa listagem, basta calcular a probabilidade solicitada no exercício.


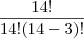 .
.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.